Question
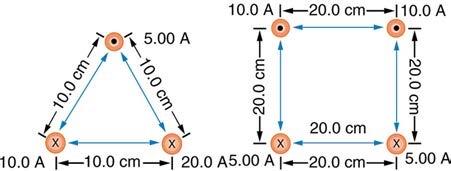
What current is needed in the top wire in Figure 22.58(a) to produce a field of zero at the point equidistant from the wires, if the currents in the bottom two wires are both 10.0 A into the page?
Final Answer
into the page.
Solution video
OpenStax College Physics, Chapter 22, Problem 71 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We're told to consider wires arranged as they are in this picture here, but the bottom two wires both have a current of ten Amps, so this wire three has ten Amps instead of 20 Amps. And we're meant to find out what current is needed in wire one such that the resultant magnetic field in the center of this triangle is zero. Now the magnetic fields created by wires three and two are going to be directed like this, that's shown in blue because if you place your thumb into the page at wire three in the direction of the current. And then, your position of your fingers in the middle of the triangle are going to be pointing up into the right and so that's what this vector shows. And then for wire two, your thumb goes into the page and here your fingers point down to the right. And so these two magnetic fields are going to have equal but opposite directed Y components because they have the same size current and they are the same distance from this point. And this is an equilateral triangle. And so their angles are the same. And this is 60 degrees and this is also 60 degrees. And so the Y components are going to cancel which means for wire one, we want magnetic field which points straight to the left in order to cancel the X component of B3 and B2 that are added together. Now the X component of B3 and B2 are going to be of equal magnitude. And so this magnetic field due to wire one that we want is going to be two times the X component of one of the other wires. And so that's two times B2 times cos 60. I suppose I should explain why that 60 degrees is there. Consider this line here, we call that the transfers between these two parallel lines. One being the bottom of the triangle, the other being just as horizontal. And we know that a line connecting a corner of an equilateral triangle to the center is going to bisect this 60 degree angle here. And so this is going to end up being a 30 in here. And since in yellow these are two parallel lines, that makes this angle here and this angle here between the horizontal and the transfers are interior angles. And interior angles add up to 180. And we know this is 90 degrees because this is the field due to wire two and it is tangent to a circle, centered at wire two and a tangent radius angle is always 90. And so if this is a 90 and this is a 30 and of these have to add up to 180, at least 60 left over for here. And the same idea applies up there too. So, let's see, we have magnetic field two is going to be Mu naught current two divided by two Pi r and magnetic field due to wire one at the top there is going to be Mu naught current one divided by two Pi r and the r is the same for all the wires cause they are all equally distant from the center. And then we can make substitutions in this formula using these in green. And so the substitutions are done in red. So Mu naught I1 over two Pi r equals two times I guess may be over here, actually, two times Mu naught I2 over two Pi r times cos 60. And the whole bunch of things cancel on both sides. The Mu naught and two Pi r is cancel. Meaning that I1 is two times I2 times cos 60. Now cos 60 is part of one of our special triangles. We have 30-60-90 and one side is of length one two and root three. So cos of 60 is a half and so this works out to 10.0 Amps into the page. If you don't like that special triangle, you could just go two times ten Amps times cos 60 in your calculator and you'll end up with ten. And it has to be in the page because in order for the fields to be going to the left here due to wire one, you need to put your thumb into the page in order to have their fingers pointing to the left there. And so that's another difference in this drawing, its current has actually going to be into the page.