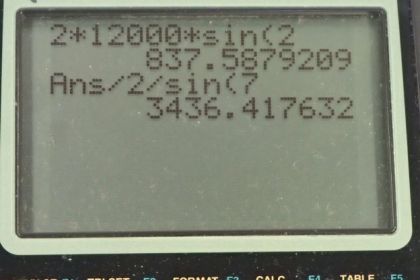
Question
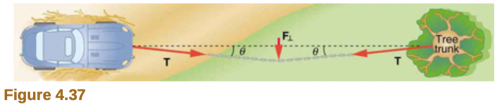
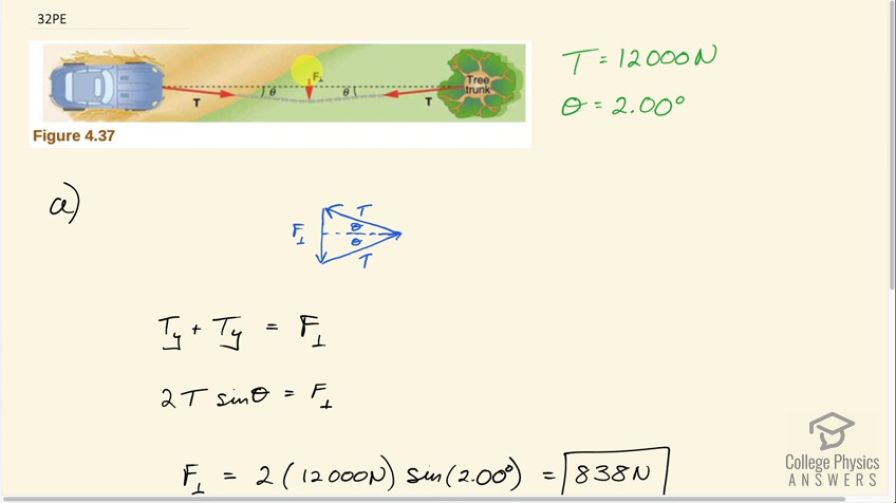
Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure 4.36 to pull it out. (a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is ? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. (b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to and you still apply the force found in part (a) to its center?
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 32 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a car attached to a tree by this rope. And then there's a perpendicular force applied in the middle of the rope in order to create some tension in the rope. And the tension we're told is 12000 newtons. And this angle theta here between the line connecting the car to the tree and the rope is two degrees. So we need to figure out what this perpendicular force is, given this tension in the rope and given this angle. So I'm drawing a vector triangle here, where we have the three forces that are acting at this particular point here. This tension is away from the tree, but we can also think of it as being away from the central point as well towards the tree. Tension acts along the rope in both directions. And likewise, there's a force acting away from this point of the perpendicular force towards the car. And these three forces added together are shown in this triangle here. And they’ll have to add up to zero, which is to say that the resultant is just where we started. Because there's no acceleration of the system. So, we have the perpendicular force straight down. We have this tension force along this line here, that represents this one connected to the tree. And then I'm putting the tail of this force towards the car on the head of the tail, or on the head of the vector towards the tree. And we end up here. Okay. The horizontal forces balance out. But let’s concern ourselves with the vertical forces. Since there's no acceleration here, we know that the total force upwards has to equal the total force downwards. So we put them on opposite sides of this equation. We have one y-component of tension upwards, and then we have another y-component of tension upwards. And those two together have to equal the total perpendicular force downwards. And each of these tension forces is the tension force multiply by sine of the angle theta, because it’s this opposite leg that we're concerned with. This is t subscript y just this portion here. And since it’s the opposite leg, you use the sine function multiplied by the hypotenuse to find it. And there's two of them, so that's why we’re multiplying by two here. So the perpendicular force then is two times the tension, 12000 newtons times sine of two degrees, which is 838 newtons. Now, what if the angle was instead seven degrees instead of two with the same perpendicular force? What will the tension be in that case? Well we can take this equation and solve it for tension by dividing both sides by two sine theta. Then we get the tension is, perpendicular force divided by two sine theta. So that’s 837.59 newtons divided by two times sine 7 degrees, which is 3.44 times ten to the three newtons.
Comments
For Part B on your calculator's screenshot it shows that you have divided you answer by 2 then divided that again by sin(7°), but in your formula it show that you should divide by 2*sin(7°), so then wouldn't the answer be 209N?
Hi samuelh, thank you for the question. The issue here is knowing how the calculator "thinks" -> it works from left to right so it evaluates the "divide by 2" first, then takes that answer and divides by . This is the same dividing the top by the answer of but requires fewer button pushes since I don't need to enter the brackets around the . My personal preference is for fewer button pushes, which I hope doesn't create too much confusion!
All the best,
Shaun