Question
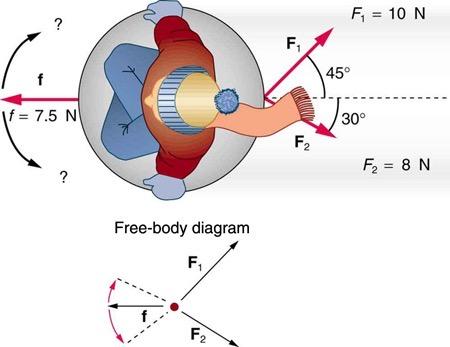
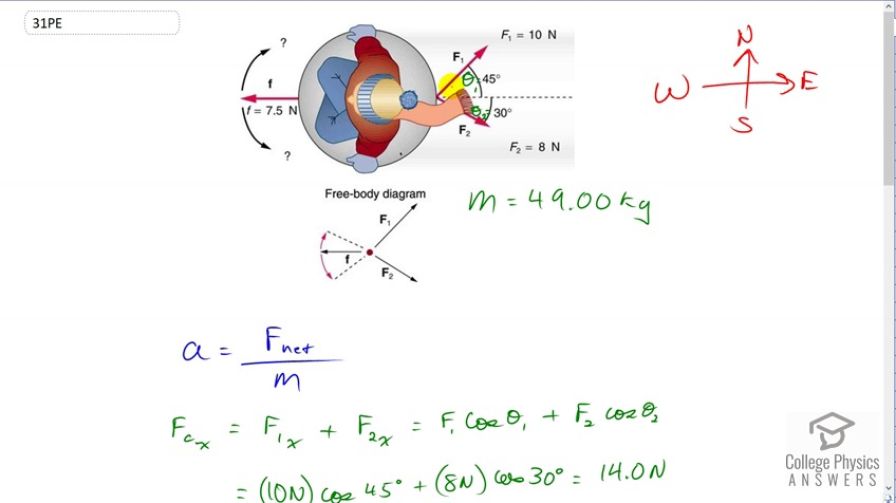
Two children pull a third child on a snow saucer sled exerting forces and as shown from above in Figure 4.35. Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of and .
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
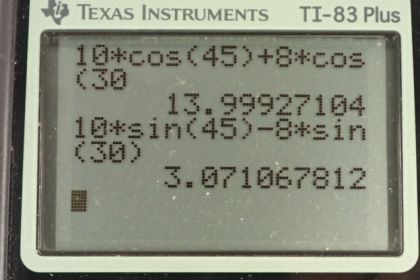
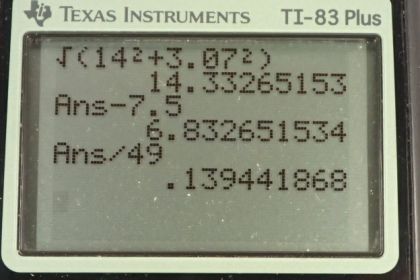
This is College Physics Answers with Shaun Dychko. Our job in this question is to figure out the acceleration of this child on the saucer. He’s being pulled by one child with a force of ten newtons 45 degrees North of East, and then child two is pulling with a force of eight newtons 30 degrees South of East. There’s a friction for us but it doesn’t show us exactly what the direction of that is because it will be exactly anti-parallel or the opposite direction to the net force of these two and we haven’t figure out what that is yet. So the acceleration of the child’s saucer system will be the size of the net force divided by the mass of the child and the saucer. First of all we’re going to find out what the total forces exerted by the children are which is not strictly speaking the net force because this will get us the total x component of these two forces to the right and there’s also a component of friction which is to the left. We’ll deal with that in a second. So first of all we’re just gonna add these two forces F1 and F2 together and we’ll call that Fc for total child force. So that’s the x component of force one plus the x component of force two and they are both positive and to the right. And so the x component of force one is F1 times the cosine of angle one because we’re looking for the adjacent leg of this triangle here and then likewise for force two, we’re multiplying it by cosine of theta two. That is ten newtons times cos 45 plus eight newtons times cos 30 which gives 14.0 newtons. The total force exerted by the two children in the y direction is F1y which is positive and upwards minus F2y, and it’s a minus because it is directed downwards, and that’s the opposite leg of each of these triangles here so we’re going to use the sine function to find it. So that’s ten newtons times sin 45 for the y component of force one minus eight newtons times sin 30 which gives 3.07 newtons. So the total force exerted by the children then is the square root of the sum of the squares of the components, so that’s square root of 14 squared plus 3.07 newtons squared, which gives 14.33 newtons. So that’s the total force exerted by the two children. Now the force of friction is going to directly oppose that so it can be subtracted directly from it and then this will give us the net force on the child saucer system. So that’s 14.33 newtons minus the 7.5 newtons that we’re told is the friction force, which is 6.833 newtons. So the acceleration will be the net force divided by the child saucer mass so that’s 6.833 newtons divided by 49 kilograms which is 0.14 meters per second squared. Then we’re going to find the angle of this acceleration. It’s going to be directed in the same direction as the total force applied by the children because this friction force doesn’t have any effect on the direction because it’s always going exactly opposite to the direction of motion. So we have inverse tangent of 3.07 divided by 14 which is 12 degrees North of East. We know it’s North of East because the y component of this total force exerted by the children is positive so that’s Fcy. Then Fcx is something to the right and so this is the total force exerted by the children and the angle we’re finding right now is here, theta. So by taking the inverse tangent of this over this, we’re finding this angle which is to the North of East. If you look here it’s to the North of East. So there we go, final answer is 0.14 meters per second squared, 12 degrees North of East.