Question
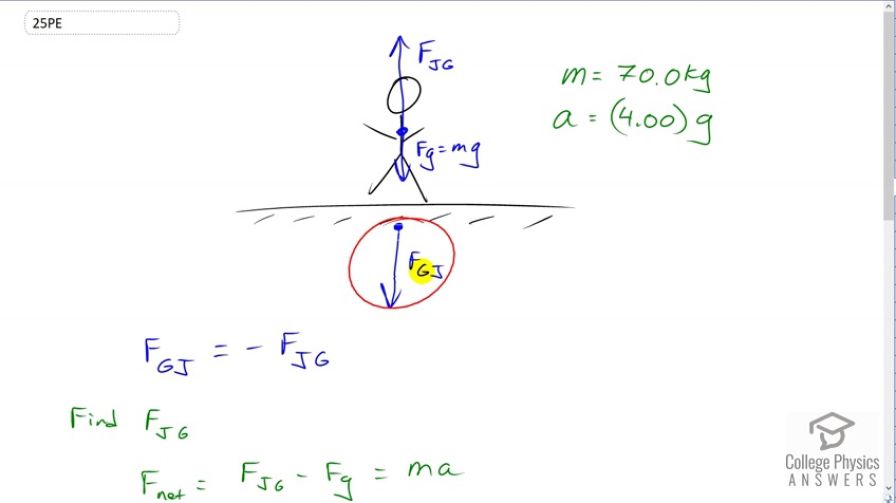
Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are asked to find the force that the jumper exerts on the ground and that's labeled here, this is the force on the ground due to the jumper, but to find that we're going to need to figure out the third law counterpart to this force instead. So that is the force on the jumper due to the ground. But they're equal in magnitude, just in opposite directions, these Newton's third law pairs. So we've drawn a free body diagram which is a really good step in our problem solving strategy, written down the things that we know. The mass of the jumper is 70 kilograms, the acceleration will be four times acceleration due to gravity, and then we'll write down the net force, the force upwards minus the force downwards equal mass times acceleration. So this is the force on the jumper due to the ground, minus the force of gravity. Then add fg to both sides because we want to solve for this. So we have the force on the jumper due to the ground is mass times acceleration plus the weight, and that is mass times four times g since that's what the acceleration is going to be, plus mg. So these two terms have a common factor mg and so you can factor the mg out and you have mg times four plus one which is five mg. So the force on the jumper due to the ground is five times the jumper's mass, 70 kilograms, times the gravitational field strength of 9.8 newtons per kilogram which is 3430 newtons. The magnitude of the force on the ground due to the jumper is the same as the magnitude of the force on the jumper due to the ground because of Newton's third law pairs and that is 3430 newtons. The last step in your problem-solving strategy is to check whether your answer is reasonable and so let's compare that to the weight of the jumper, 70 times -- well 9.8 is roughly 10. So this divided by 700 is about 5 and it seems reasonable that a jumper could exert 5 times their weight.
