OpenStax College Physics, Chapter 4, Problem 27 (Problems & Exercises)

A freight train consists of two

8.00 \times 10^4 \textrm{ kg}

engines and 45 cars with average masses of

5.50 \times 10^4 \textrm{ kg}

. (a) What force must each engine exert backward on the track to accelerate the train at a rate of

5.00 \times 10^{-2} \textrm{ m/s}^2

if the force of friction is

7.50 \times 10^5 \textrm{ N}

, assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?

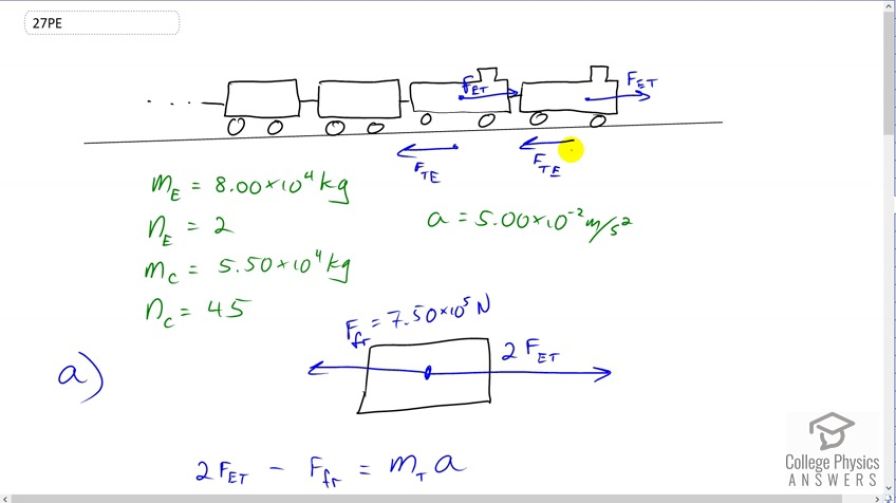
This is College Physics Answers with Shaun Dychko. Part A of this question is asking us to figure out the force exerted on the track due to the engine. Now to figure that out, we need to look at its Newton's third law counterpart which is the force on the engine due to the track because this we can figure out since we're given some information about the train, its acceleration, and its mass, and so on. So there's going to be two engines, each exerting a force on the track and so therefore the track is going to exert an equal and opposite force on each of the engines. So the total force to the right is going to be two times that force on the engine due to the track. So in this picture down here I've simplified our free body diagram to summarize this whole train as a single body experiencing a total force to the right of two times F et, and a total force of friction to the left which we're given. Now writing down the other information we know, we know there are two engines, so the number -- that's what n stands for, number of engines, is two and each engine is eight times ten to the four kilograms. We're told the number of cars is forty-five, each of them weighing or having a mass of 5.5 times ten to four kilograms. So let's figure out the force on the engine due to the track and then at the end we'll say, well the force on the track due to the engine is of equal magnitude because they are Newton Third law pairs, and there we go! So, second law, Newton's second law, net force is mass times acceleration so we have to the right two times the force on each engine due to the track, minus the total friction force to the left, equals the total mass of the train multiplied by its acceleration. The total mass of the train will be forty-five times the mass of each car, plus two times the mass of each engine. So we make a substitution for that and we do that here in red. We have -- well, we're also adding friction to both sides to solve for F et. So we have two F et equals total mass times acceleration plus friction and that's forty-five times mass of the cars plus two times mass of the engines times acceleration plus friction. Then divide both sides by two and you get this line here where you've made substitutions for each of these variables. So we have the force on the engine due to the track is going to be forty-five times 5.5 times ten to the four kilograms, mass of each car, plus two engines times 8 times ten to the four kilograms of mass for each engine, and all that gets multiplied by the acceleration which we're given as five times ten to the minus two meters per second squared. Then add to that the force of friction, 7.5 times ten to the five newtons, and divide that whole result by two. You get 4.41 times ten to the five newtons is the force on the engine due to the track and since the force on the track due to the engine is the Newton's third law counterpart, it is of the same magnitude 4.41 times ten to the five newtons. Then in part B, it says, what is the force in the coupling between the thirty-seventh and thirty-eighth car? So we consider this body just to the left here then. It has a force due to the coupling going to the right, so that's F subscript c and then it has a force of friction going to the left. But I put an apostrophe here or a prime because this is not the same force of friction as up here. Because this force of friction we assume according to the question is evenly distributed among all the different cars and engines. So the force of friction here will be the force of friction per thing, so we're taking the total force of friction and this one has no prime. This is this one up here, divided by the total number of things, so the number of cars plus number of engines and that's the friction per thing, and then multiplied by the number of cars that we have here where this is n c which is prime because I used the n c variable up here to mean forty-five but down here it means 8 because there are eight cars after the thirty-seventh car. The mass of the system here is the number of cars, 8, times the mass per car. Okay. So the net force in this new question, so that's why it's a prime 'cause it's part B, it's a different net force than we had in part A, is the force in the coupling to the right minus the Fr prime, force of friction to the left in this case. That equals the mass of this system of eight cars, times its acceleration. Acceleration does not get a prime because it is the same acceleration as we had in part A. Then we'll solve this for Fc by adding F fr prime to both sides and we get the force in the coupling is the mass prime, times acceleration, plus force of friction prime. The mass prime is the number of cars which is eight times the mass of each car and then the force of friction. I made a substitution from here, in there. Then factor out the common factor n c prime, and we end up with 8 which is the number of cars here, times 5.5 times ten to the four kilograms, mass of each car, times 5 times ten to the minus two meters per second squared, acceleration of the system, plus the force of friction in total divided by the number of cars plus engines. We end up with 1.5 times ten to the five newtons is the force required to pull this whole system to the right, consisting of eight cars. So that must be the force in the coupling.