Question
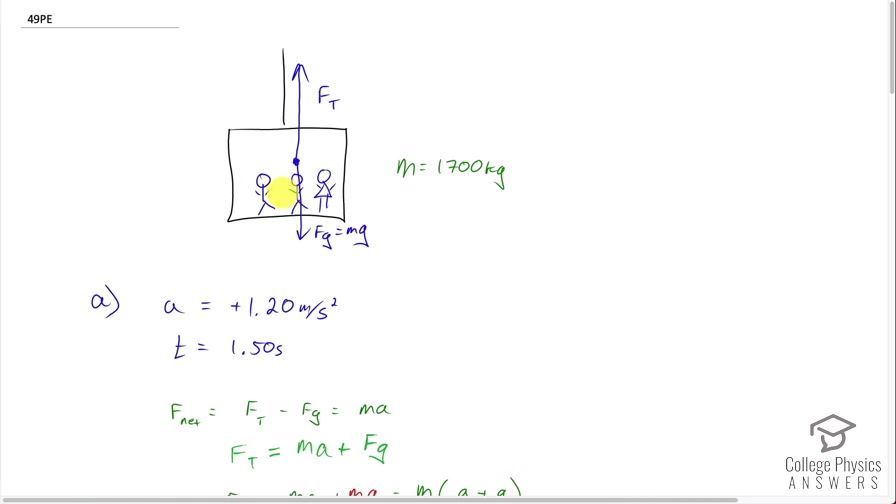
Integrated Concepts An elevator filled with passengers has a mass of 1700 kg. (a) The elevator accelerates upward from rest at a rate of for 1.50 s. Calculate the tension in the cable supporting the elevator. (b) The elevator continues upward at constant velocity for 8.50 s. What is the tension in the cable during this time? (c) The elevator decelerates at a rate of for 3.00 s. What is the tension in the cable during deceleration? (d) How high has the elevator moved above its original starting point, and what is its final velocity?
Final Answer
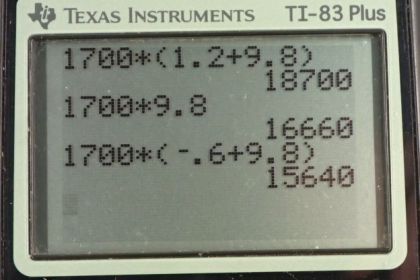
a)
b)
c)
d) ,
Solution video
OpenStax College Physics, Chapter 4, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have an elevator full of some passengers and we are told that the total combined mass of elevator plus passengers is 1700 kilograms. There's a tension force applied upwards due to this cable and there is gravity downwards and that makes up our free body diagram—only these two forces that we are concerned with. The elevator will have three intervals to its motion— the first interval of time, it's going to be accelerating upwards for 1.50 seconds and then it will be moving upwards at constant speed for 8.50 seconds and then it decelerates for 3.0 seconds. So in each part, we are going to figure out what is the tension force in this cable? And then in the last part of this question, part (d), we will figure out what is the total distance the elevator has traveled and what will its final speed be? So an expression for the force of gravity is mass times gravitational field constant, g, in part (a) of this question, we are going to consider the first 1.50 seconds when it's accelerating upwards at 1.20 meters per second squared and let's find the tension force. So the net force has to be the total forces— that's tension upwards minus gravity downwards and that equals mass times acceleration— and we can solve for tension force by adding force of gravity to both sides so I do that here and then we are left with tension on the left equals mass times acceleration plus force of gravity on the right. We can substitute mg in place of F g and then factor out the common factor m between these two terms and we are left with the tension force is the mass times acceleration plus acceleration due to gravity. So that's 1700 kilograms times 1.20 meters per second squared plus 9.80 meters per second squared and that's 1.87 times 10 to the 4 Newtons— that's the tension force in the cable. Okay! In part (b), we are told that there's no acceleration and this goes on for 8.50 seconds and the question is what is the tension force now? Well the net force expression is the same— a free body diagram has tension upwards and gravity downwards— and that still equals mass times acceleration because that's what net force always equals and this is now 0 because acceleration is 0. So we can solve for F T again by adding F g to both sides and we are left with the tension force equals gravity. So the tension force is 1700 kilograms times 9.8 Newtons per kilogram and that is 1.67 times 10 to the 4 Newtons. You might notice that I had units of meters per second squared here for g in part (a) and then I had units of Newtons per kilogram in part (b)— those units are equivalent and you can choose whichever one makes more sense depending on the situation. So in this question, we are adding an acceleration to an acceleration so I might as well keep these units the same— meters per second squared— whereas down here I am multiplying by kilograms and I want to end up with the force so it makes more sense to use Newtons per kilogram as the units here. Okay that's just a personal preference thing... you don't have to do that but just so you know that it's possible. Okay! 1.67 times 10 to the 4 Newtons is the answer here. In part (c), we have a deceleration or in other words, an acceleration directed downwards and that is the negative direction so our acceleration is negative 0.600 meters per second squared for 3.00 seconds and the tension force, you know, just the same as before I took a shortcut here but it's the same working as up here where we have F T minus F g equals ma and then move the F g to the right hand side and factor out the m so I am starting here and here. So tension force is mass times the sum of the acceleration of the elevator plus acceleration due to gravity. So we substitute in 1700 kilograms times negative 0.600 meters per second squared plus 9.8 meters per second squared and the tension force is 1.56 times 10 to the 4 Newtons. And we expected a tension force that is less in part (c) than in part (a) because you know gravity is winning in part (c)— the elevator is accelerating downwards— whereas in part (a), tension force is causing it to accelerate upwards and so it would have to be that much greater than gravity to do that. Okay! Always good to do a bit of a reality check on your final answers to see if they roughly make sense with sort of a conceptual understanding of the question. Part (d) asks us what is the final height of the elevator. So we consider time zero at the very beginning— we'll call that y naught— and that's our initial position and that's going to be y naught equals 0— that's our reference level, you could say— and then we will get to this position here—y 1— after the first interval of time, which is 1.50 seconds during which we have acceleration a 1 of 1.20 meters per second squared and we have to split this up into three sections because our formula here is true only when you have constant acceleration. So the acceleration is changing in this question which means you cannot use this formula one time and expect to get an answer. Instead you have to use it for each period of time during which acceleration is constant so it's constant here from 0 to y 1 and then it's constant again from y 1 to y 2 during which time it is 0. And then from y 2 to y 3, the acceleration is constant at negative 0.600 meters per second squared and we assume that, just for simplification, that the transition between these accelerations is instant. Okay! So first let's figure out what is y 1? y 1 is the y naught plus v naught t plus one-half a 1 times this interval of time t 1 squared. So y naught is zero because that's our reference level v naught is also zero... it starts from rest and so we are left only with one-half a 1 times Δt 1 squared. So that's one-half times 1.20 meters per second squared times 1.50 seconds squared and that's 1.35 meters. So we can right now say that this is 1.35 meters—that y 1. Okay! y 2 is going to be the initial height for this time period and the initial height for the y 2 time period is y 1 so that's why I put y 1 here. So y 2 is y 1 plus the speed at which the elevator is traveling when it reaches this position here y 1 plus one-half times the acceleration during interval 2 times Δt 2 squared. Now there's no acceleration during interval two— a 2 is 0— so this term disappears and we are left with y 1 plus the acceleration during interval one times the time period Δt 1 because this is telling us the final speed after the elevator reaches y 1 and we multiply that by the interval of time Δt 2. So that's 1.35 meters—y 1— plus 1.20 meters per second squared times 1.50 seconds times 8.50 seconds and that is 16.65 meters so the total change in height up to here is 16.65 meters. Okay! There we go! And then finally y 3 is the next question. So y 3 equals y 2 because y 2 is the initial position during this interval of time Δt 3 and you are going to add to that the speed it was going when it started here at y 2 and which, incidentally, would be the speed at y 1 as well since there is no acceleration during interval two so you will see that we end up putting a 1Δt 1 in place of v 2 here. We multiply that by Δt 3 and then add to that one-half times acceleration during interval three times Δt 3 squared. So that's 16.65 meters—y 2— plus 1.20 meters per second squared times 1.50 seconds— that's the final speed at the end of time one and time two— times 3.00 seconds during time interval three plus one-half times negative 0.600 meters per second squared times 3.00 seconds squared and that's 19.35 meters. So that is the final height of the elevator: 19.35 meters... from here to here. Okay! Good! And then the next part of the question is what is the final speed? So the final speed will be the initial speed, which is 0, plus Δv 1—the change in speed during interval 1— plus Δv 2—the change in speed during interval 2— and Δv 3—the change in speed during interval 3. So the initial speed is 0, the change in speed during time interval 1 is a 1—acceleration—times Δt 1 and then there's no change in speed during interval two because the acceleration is 0 and then add to that the change in speed of interval 3 which is a 3 times Δt 3. So that's 0 plus 1.20 times 1.50 seconds plus 0 plus negative 0.600 meters per second squared times 3.00 seconds and this all adds up to 0 as it turns out which means that the elevator must have arrived at its destination floor and the passengers can get out now after the doors open.
Comments
Hey there Shawn, I believe answer A should be 10 to the 4th power or 18700N (16660 N + 2040N=18700N)
That first answer should be 18700, not 1870.
Hello, thank you so much for noticing this! I have corrected the final answers and made a note about the error in the video, and flagged the video for a re-do.
The video was updated on Nov. 30th, 2023.