Question
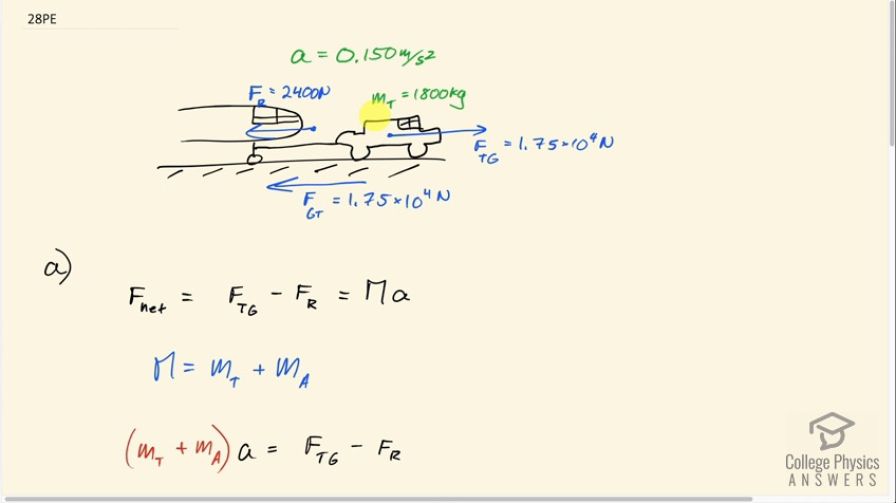
Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is , what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.
Final Answer
- Solutions should always have such sketches! See parts (a) and (b) in the solution video.
Solution video
OpenStax College Physics, Chapter 4, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
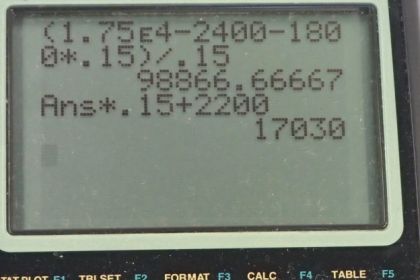
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A tractor is attached to the front wheel of a plane and pulling it out of the gate. And the mass of the tractor we’re told is 1800 kilograms. The tractor is applying a force of 1.75 times ten to the four newtons on the ground. So this is labeled f subscript g for ground and t for tractor; the force on the ground due to the tractor. And this is relevant, because it tells us what the force on the tractor due to the ground is. Because these are Newton’s third law counterparts. So the force on the tractor due to the ground is to the right. And it is of the same magnitude, 1.75 times ten to the four newtons. The total force of resistance on the system is 2400 newtons, and notice that I wrote the origin of this vector, sort of in the space in between the plane and the tractor. And that's intentional, just to say that this is a force on the system, is not just on the plane or just on the tractor. You can also think of this force as being the same. I could have written this one over here as well. So we have two forces on this system, where the system is considered this whole, this pair of a vehicles is one thing. So the net force on the system is; its total mass times acceleration. And I wrote mass with a capital m just to emphasize that this is the total mass; the mass of the tractor plus the mass of the airplane. And the net force then is the force to the right, which is the force on the tractor due to ground and then minus the force to the left, which is the resistance force that were given. So we switch the sides around and substitute capital m with mass of the tractor plus mass of the airplane. And that's times acceleration equals the difference in forces. And then distribute the acceleration into the brackets there, multiplying both terms by it. And then we get m t a plus m a a equals f t g minus f r. And then we’ll subtract mass of the tractor times acceleration from both sides. And then we have the mass of the airplane almost isolated on the left. It’s still being multiplied by this factor a. So we’ll divide both sides by a to isolate the mass of the airplane completely. So it’s the force on the tractor due to the ground, minus the resistance force, minus the mass of the tractor times acceleration, all divided by acceleration. So that’s 1.75 times ten to the four newtons, minus 2400 newtons, minus 1800 kilograms; mass of the tractor, times the acceleration of .15 meters per second squared. All divided by the acceleration. And that gives 9.89 times ten to the four kilograms as the mass of the airplane. Then in part B we’re told, suppose the airplane specifically experiences a resistance force. Or force of friction in other words of 2200 newtons to the left. What force must the tractor be apply on the plane? And we’ll calculate that knowing that the plane has this acceleration, the same as before .15 meters per second squared. And then we'll use Newton’s second law to figure out what this force must be. So the net force is the force due to the tractor, minus the force due to friction, equals the mass of the airplane times acceleration. And notice this mass is only that of the airplane. Because now our system consists only of the airplane, doesn't consist of the tractor. Sure, there's a force applied by the tractor, but that is of course that’s on the plane. Okay, so we’ll add the force of friction to both sides. And then we have the force of the tractor isolated. It’s the mass of the airplane times it’s acceleration plus this friction force that he experiences. So here is the mass of the airplane calculated in part A multiplied by .15 meters per second squared acceleration, plus 2200 newtons. Gives 1.70 times ten to the four newtons. In part C, asks us to draw a free body diagrams of the systems in each of these parts A and B. But you should always have sketches like that as I do and we are just look at parts A and B for those sketches. And they're very helpful in creating your solution and organizing your thinking and making sure that you understand the situation.