Question
Show that, as stated in the text, a force , exerted on a flexible medium at its center and perpendicular to its length (such as on the tightrope wire in Figure 4.17) gives rise to a tension of magnitude
Final Answer
see video for derivation.
Solution video
OpenStax College Physics, Chapter 4, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
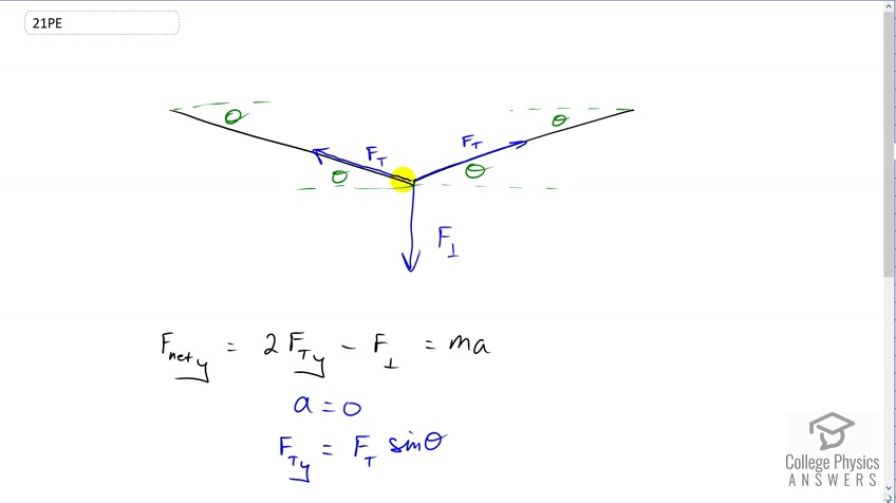
This is College Physics Answers with Shaun Dychko. Given a force perpendicular exerted on this flexible medium or a rope, for example, we're going to figure out what is an expression for the tension force given this angle and this perpendicular force. So it's perpendicular to the length here of the flexible thing so it's exerted this way which is a right angle right there. So the net force in the y direction is two times the y component of the tension force because this tension force has a y component here. It also has a y component on the other side and so these add together to make the total force in the upward direction and then minus the force downwards, all of that equals mass times acceleration in the y direction, which there is none because we're told that this thing is static or motionless. We can also find an expression for the y component of the tension force in terms of the tension in this angle because this is the opposite leg of this triangle. So we'll use sine of theta multiplied by the hypotenuse to get the opposite leg. So we have Ft sine theta is the y component of Ft. So now we copy this formula here again but we make substitutions. So substituting for a being zero means that the right hand side is zero, and then substituting for Ft y as Ft sine theta, we get this line. So we have two times Ft sine theta minus F perpendicular equals zero, and then add perpendicular force to both sides. Then it disappears on the left leaving us with two Ft sine theta equals F perpendicular and then to solve for Ft, divide both sides by two sine theta. This gives us our expression. So the tension force will always be the perpendicular force divide by two times sine of the angle.