Question
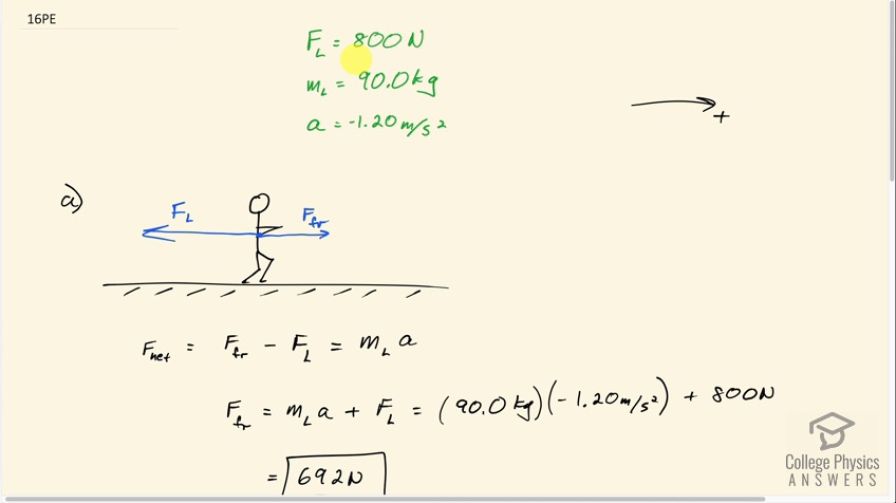
A brave but inadequate rugby player is being pushed backward by an opposing player who is exerting a force of 800 N on him. The mass of the losing player plus equipment is 90.0 kg, and he is accelerating at backward. (a) What is the force of friction between the losing player’s feet and the grass? (b) What force does the winning player exert on the ground to move forward if his mass plus equipment is 110 kg? (c) Draw a sketch of the situation showing the system of interest used to solve each part. For this situation, draw a free-body diagram and write the net force equation.
Final Answer
- See figures in parts (a) and (b).
Solution video
OpenStax College Physics, Chapter 4, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A rugby player experiences a force opposing the direction they want to go of 800 newtons. Their mass is 90 kilograms and they're having an acceleration in the negative direction 1.2 meters per second squared. We're going to take right to be the positive direction and I have the subscript L to denote the losing rugby player. This is their force then and this is their mass. The net force on this player is going to be the force of friction positive to the right, that's the friction force exerted by the ground on the player. Then to the left, which is why I have a minus here, we have this applied force 800 newtons, and all of that equals the mass of the losing player times acceleration. Now I usually put negative signs explicit on the force side of the equation for for Newton's second law, and so that means these forces are all magnitudes and their direction is taken care of by putting a plus or a minus in front of them. The acceleration on the other hand, I don't do that and so there is an implicit negative 1.2 contained within the letter A here. Okay, so we're going to solve for this friction force and we'll add the force applied on to the losing player by the winning player to both sides. We have the friction force then as m La plus F L It's 90 kilograms times negative 1.2 meters per second squared acceleration plus 800 newtons giving 692 newtons as the force that the ground applies on this player. In part B, we need to consider both players together as a system. Acting to the right on the system is this force we just discovered in part A, that's the force of friction on the losing player, but they're connected to the winning player and so we'll think of it all as one big thing. There's 690 newtons to the rate on that thing and then we're going to figure out what this forces to the left, which will be the force that the ground applies on the winning player. This w g, this denotes the force on the winning player due to the ground. The question asks for the force on the ground due to the winning player, but those are Newton's third law counterparts and so that means they're magnitudes are the same. So if you figure out the magnitude of this force, that'll be the same as the magnitude of the force on the ground due to the winning player. The mass of the system is the mass of the losing player plus the mass of the winning player, that's 90 plus 110, making 200, and the acceleration is just the same as in part A. The net force is going to be the force to the right minus the force to the left, and that equals the total mass times acceleration and will solve for F wg by adding it to both sides and then subtracting ma from both sides, and switching the sides around. So we have the force on the winning player due to the ground is the force that the ground applies on the losing player to the right, minus total mass times acceleration. So 692 newtons minus 200 kilograms times negative 1.2 meters per second squared acceleration, giving a force of 932 newtons. In part C, it says draw some pictures, but I always draw pictures for my solutions and so you just have to look at parts A and B.
