Question
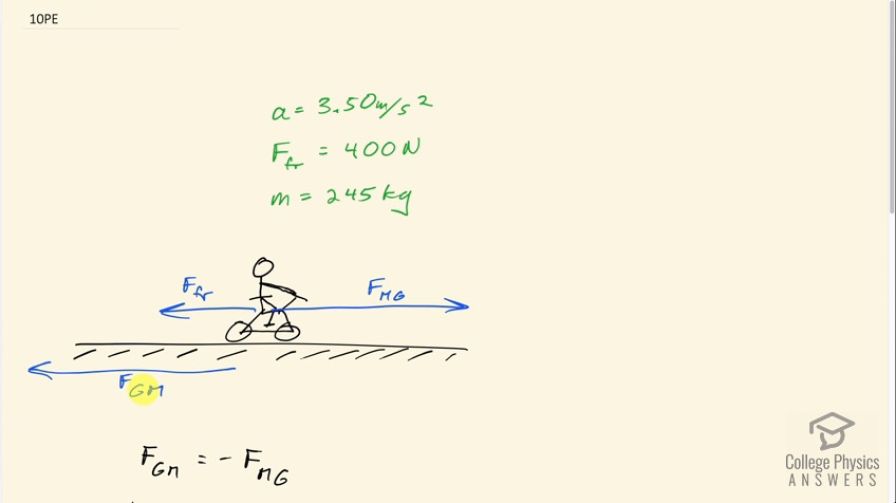
A powerful motorcycle can produce an acceleration of while traveling at 90.0 km/h. At that speed the forces resisting motion, including friction and air resistance, total 400 N. (Air resistance is analogous to air friction. It always opposes the motion of an object.) What is the magnitude of the force the motorcycle exerts backward on the ground to produce its acceleration if the mass of the motorcycle with rider is 245 kg?
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us what magnitude of force does a motorcycle apply backwards on the ground? What is the force on the ground due to the motorcycle in other words. Well, this is a Newton's third law counterpart to the force on the motorcycle due to the ground. I have m standing for a motorcycle and the g subscripts and for ground. So if we can figure out what this force is, then this force that we want going to have the same magnitude. We've written down the stuff that we know, we know the acceleration is going to be 3.5 meters per second squared. The force of drag or air friction is 400 Newton's going back and the mass of the rider and motorcycle is 245 kilograms. Here, I've written down what I was saying about how the force on the ground or the motorcycle is the opposite of the force on the motorcycle due to to the ground, and you can say that their magnitude then, the absolute values in other words, are the same. Let's write down newtons second law here, that the net force, which is the force on the motorcycle due to the ground to the right is positive, and then minus the force of friction to the left, all of that equals mass times acceleration. We can solve her F mg by adding force of friction to both sides. Notice that some teachers prefer to put a plus sign here in this Newton's second law, because strictly speaking, you are adding the forces, which I'm doing too, but I prefer to have minus signs explicit in this algebra rather than having them buried inside the terms. Either way, you're going to get the same answer. We have the force on the motorcycle due to the ground is 245 kilograms, multiplied by 3.5 meters per second squared, plus 400 newtons which is 1,260 newtons, and the magnitude of the force on the ground due to the motorcycle is going to be the same as this magnitude and so it is also 1,260 newtons.
