Question
Integrated Concepts A 2.50-kg fireworks shell is fired by a mortar at an angle from the vertical and reaches a height of 110 m. (a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 48 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
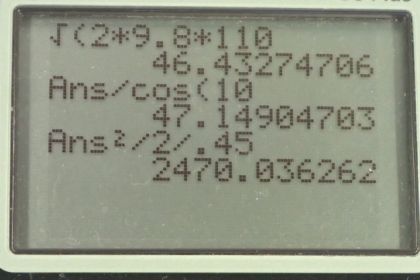
This is College Physics Answers with Shaun Dychko. This mortar has been launched at an angle of 10 degrees with respect to the vertical. Theta is a bit different than what we're used to in these projectile questions. Normally we have data is with respect to the horizontal here but in this question, they've made it with respect to the vertical. Let's keep that in mind. We know the mass of a firework is two and a half kilograms and has a maximum height of 110 meters. In part A, we figure out what is the initial launch speed here and I suppose I should label this V naught. We have this kinematics formula, which says at the final velocity squared is the initial velocity squared, and in the vertical context, we can say this is the vertical component of the initial velocity. This is the final vertical component of its velocity which will be zero at the maximum height and that's what we see here. Then minus 2 times the acceleration due to gravity times the final height minus the initial height. We take the initial height to be zero and the final height is this maximum that we're given. We substitute all these things that we know into our regular formula here, and we get zero equals Vy naught squared minus 2g times y max minus zero. We can bring this term to the left hand side by adding 2gy max to both sides. We get Vy naught equals square root 2gy max after we take the square root of both sides. That is the square root of 2 times 9.8 meters per second squared times 110 meters, which is 46.4327 meters per second. Now I kept lots of digits on here because this is not our final answer. This is the y-component of the initial velocity. If we were to draw the sort of velocity triangle here, but bigger so we can see it better, here's V naught that we want to find and here is V naught y-component that we have just found, and we know this angle theta here. To find V naught, e need to use cosine to get it because we know that V naught y-component equals V naught times cos theta and so we'll find V naught by dividing both sides here by cos theta. V naught is the y-component of the initial velocity divided by cosine at this angle with respect to the vertical and so that's 46.4327 meters per second divided by cos of 10 degrees which is 47.1 meters per second. Part B says imagine the inside of the mortar barrel has a final position here of 0.450 meters, and then an initial position of 0.45 meters long, in other words, and it's starting from rest. I give these velocity terms, little prime symbols here, to distinguish them from the velocity terms in part A. Because V naught that we found in part A is in fact the final velocity for part B. It's the muzzle velocity, in other words, it's the velocity with which the firework emerges from the end of this barrel. That's the final velocity in the context of part B here we're considering its movement within the barrel. The final velocity prime squared equals initial velocity prime squared plus two times acceleration inside the barrel times the change of position. We have that the initial velocity zero, its initial position is zero. We can rewrite this as 2ax equals V prime squared. We'll solve for A by dividing both sides by 2x. Tick there. Divide both sides by 2x. We get the acceleration is V prime squared over 2x. That is 47.149 meters per second squared divided by 2 times 0.45 meters, which is 2.47 times 10 to the 3 meters per second squared is the acceleration of the firework in a barrel of the mortar. In part C, we're asked what is the force applied on to the firework, and we're going to neglect gravity because we can see that the acceleration is really large. When we multiply mass by this acceleration, we get some number, an order of magnitude 3 in the thousands, whereas if you consider gravity, it's about 10 times this mass and kilograms so that's about 25 newtons which is 10 to the power of one. The force of gravity is less than the force due to the propellant in here by two orders of magnitude and so we can ignore it just to make things easier. That's two and a half kilograms times acceleration, 6.18 times 10 to the 3 newtons, and then expressing that as a fraction. To determine by what factor this is different from the force of gravity, we take that force and divide it by mg and we get 252.