Question
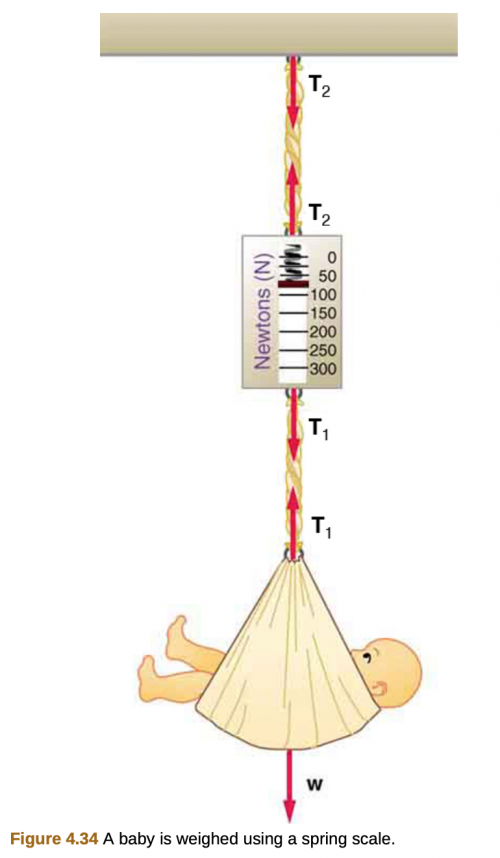
Consider the baby being weighed in Figure 4.34. (a) What is the mass of the child and basket if a scale reading of 55 N is observed? (b) What is the tension in the cord attaching the baby to the scale? (c) What is the tension in the cord attaching the scale to the ceiling, if the scale has a mass of 0.500 kg? (d) Draw a sketch of the situation indicating the system of interest used to solve each part. The masses of the cords are negligible.
Final Answer
- Please see solution video
Solution video
OpenStax College Physics, Chapter 4, Problem 22 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a baby suspended from this spring scale, and the spring scale is in turn suspended from the ceiling. And this portion of rope will have some tension force t two in it. And this piece of rope here will have some tension force t one. So this rope here supports only the baby, and this rope supports both the baby and the weight of the spring scale itself. So to figure out the mass of the baby, we know that the force upwards t one has to equal the weight downwards in order for the baby to be stationary here. And so that's why we can say; t one equals w, the force up equals the force down. And this weight is mass times acceleration due to gravity. So we can divide this by g, and this by g. And then switch the sides around to solve for the mass of the baby; which is t one divided by g. That's 55 newtons divided by 9.8 newtons per kilogram, which is 5.6 kilograms. Part B ask for the tension force and has to be 55 newtons. So because that's the force being applied upwards on the baby according to this reading on the spring scale. Part C, says figure out the tension in the top portion of rope. Given that the mass of the spring scale is .5 kilograms. So the spring scale will have a force of gravity downwards on it equal to .5 times 9.8 newtons per kilogram. And we’ll add to that the weight of the baby which is 55 newtons. And then we end up with 60 newtons as a total force t two needed to support both the spring scale and the baby. So the pictures that are required for each of these parts, part A, we consider only the baby as our system, tension force t one upwards and force of gravity downwards. And then for part B, its just this piece of rope that we’re concerning with, the tension in it. And part C, we need to consider just the spring scale and the tension force t two upwards on it and the tension force t one pulling it down, plus the force of gravity on the spring scale pulling down.
