Question
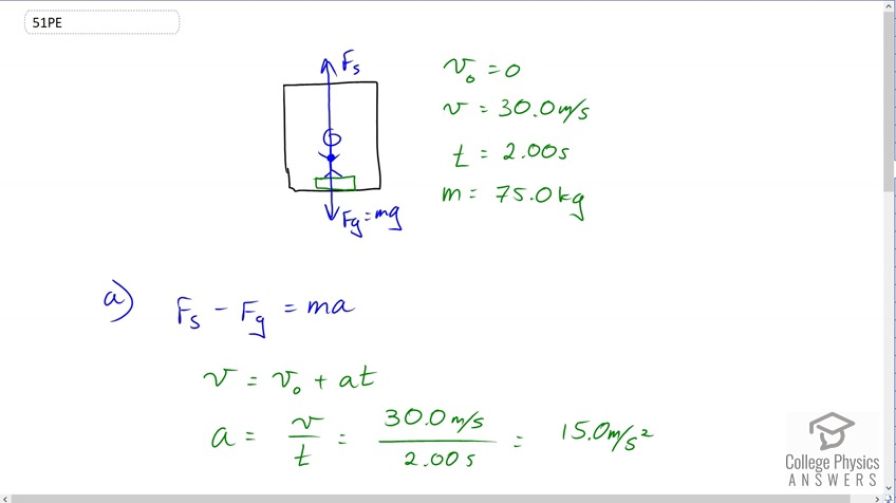
Unreasonable Results: A 75.0-kg man stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s. (a) Calculate the scale reading in newtons and compare it with his weight. (The scale exerts an upward force on him equal to its reading.) (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?
Final Answer
a)
b) The elevator acceleration is more than 2 times his weight. He will probably fall down. Elevators are not built to be so uncomfortable.
c) The final speed is too high. An elevator doesn't need to get 110 km/h.
Solution video
OpenStax College Physics, Chapter 4, Problem 51 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This man is standing on a bathroom scale in an elevator and the elevator is going upwards, it’s accelerating upwards, and over two seconds, it starts at a speed of zero and then have a final speed of 30 meters per second. The free body diagram of the man is the force upwards due to the scale, so I put a subscript s for scale and of course downwards due to gravity which is mass times gravitational field strength. So to figure out the acceleration, well to figure out the scale force, we’re going to first do this and say that the total up forces minus the total down forces equals mass times acceleration, that is the scale force minus gravity is ma. We need to figure out what this acceleration is in order to figure out the force due to the scale. So we turn to kinematics and we know that the final speed is initial speed plus acceleration times time. The initial speed is zero, we’ll divide both sides by t and then switch the sides around, we have acceleration is final speed over time. So that’s 30 meters per second divided by two which is 15 meters per second squared. So then adding Fg to both sides in the force formula, and then substituting mg in place of Fg, we have the force due to the scale is mass times acceleration plus mass times gravitational field strength. Which equals mass times a plus g, you can factor out the common factor m. So that’s 75 kilograms times 15 meters per second squared plus acceleration due to gravity 9.8 meters per second squared. Notice I use acceleration due to gravity or gravitational field strength, kind of interchangeably depending on the context, here it’s nice to call it acceleration due to gravity because we’re adding it to another acceleration but when we’re talking about the force of gravity though, when we’re calculating mg, g makes more sense to be called gravitational field strength with units newtons per kilogram because then we’re multiplying with kilograms and end up with units of newtons for force. So this gives us 1860 newtons, and then compare that to the man’s weight that is m times a plus g, force due to the scale divided by his weight which is mg and the ms cancel, so it’s a plus g over g. So 15 meters per second squared plus 9.8 divided by 9.8 and that gives 2.53. The force due to the scale is two and a half times his weight. And so he’ll probably fall down because that’s a lot of weight to support, that’s a lot of, the legs in turn have to exert a really large force upwards on his torso to keep him upright and he probably won’t be able to because this is a lot of force that would need to exert. So elevators are not meant to be uncomfortable so this is an unreasonable result and it’s unreasonable because the final speed is too high. There’s no need for an elevator to go approximately 110 kilometers an hour. That is the conversion of 30 meters per second when you multiply by 3.6. There you go. The two seconds over which the elevator accelerates, that is a reasonable number but the final speed is what’s not reasonable.
