Question
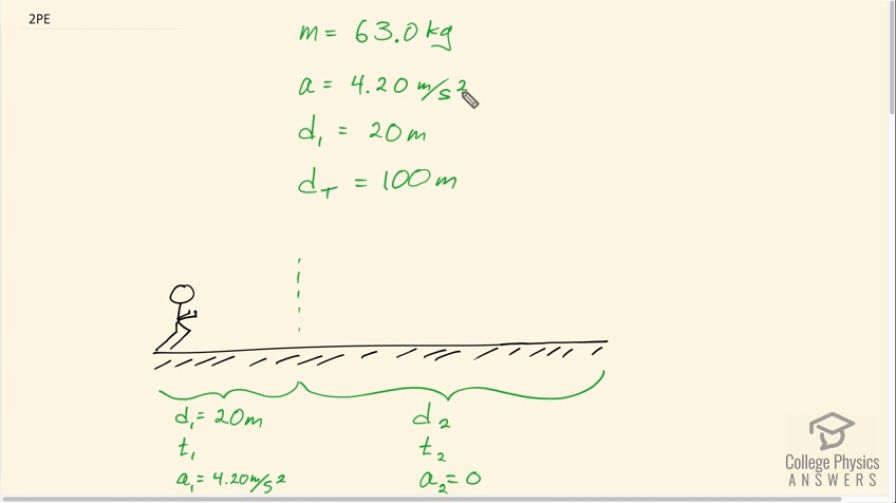
A 63.0 kg sprinter accelerates at a rate of for 20 m, and then maintains that velocity for the remainder of the 100-m dash, what will be his time for the race?
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 2 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
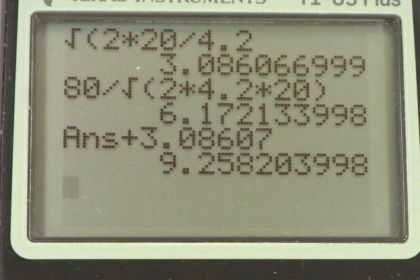
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A sprinter that has a massive 63.0 kilograms accelerates at a rate of 4.2 meters per second squared for 20 meters. We'll call that distance 1. And then after the 20 meters, they continue at whatever final speed they reached at the end of 20 meters, they continue with that constant speed for the remaining 80 meters of this 100 meter dash. The D 2 is 80 meters. Total distance is 100. The distance 1 we're told is 20 meters, and that makes D 2 total minus 20, which is good. I began by writing down all the things that we know but I've also drawn a picture which is always very helpful and drawn our knowns below the picture. For this second interval of distance, we have time to t 2 and an acceleration 2, which is zero since its constant speed. The speed that we're going is going to be V f from this first interval of time. The question is asking, what total time will it take for the sprinter to complete the 100-meter dash. What is t 1 plus t 2 In other words. We can figure out i>t 1 based on this kinematics formula here, where we say displacement one is going to be the initial velocity which is zero because they begin at rest multiplied by t 1 plus one half times the acceleration during this first interval times t 1 squared. This term disappears because the initial is zero and we switch the sides around to have the unknown on the left. Then we'll multiply both sides by 2 and divide both sides by i>a 1. Then afterwards, we'll take the square root of both sides and we end up with this line here at that time for the first interval is square root two times the first interval distance divided by the first interval acceleration. Square root of 2 times 20 meters divided by 4.2 meters per second squared, which is 3.08607 seconds. We keep lots of digits here because this is an intermediate calculation. This is a number that will add to t 2 to get a final answer, and we will not round until the very final answer. The second time interval will be the second distance divided by whatever speed they're going during that time and the speed is constant, we're told. We can figure out what the speed is because it's the final velocity achieved during the first time interval. That final velocity squared is the initial velocity squared plus 2 times the acceleration during the first interval multiplied by the displacement of the first interval, and i>V i is zero. We'll take the square root of both sides to solve for this final speed. Then substitute that in to this equation replacing V f with square root 2 a 1d 1. t 2, in other words then, that is 80 meters divided by square root of 2 times 4.2 meters per second squared times 20 meters, which is 6.17213 seconds. Add t 2 to t 1 and we get our total time which is 9.3 seconds. That has two significant figures since our distances are given with two significant figures.
Comments
where did you get the kinematic formula: d1=v1*t1 + 1/2a*t^2 ?
This is a version of equation 2.40, which you can find here: https://openstax.org/books/college-physics/pages/2-5-motion-equations-f…. The difference is that the initial position term is missing since the object is assumed to start at position zero. The "1" subscript serves as a label to say that the terms apply to the 1st portion of the race when the sprinter is accelerating.
All the best,
Shaun
Hello, would you explain how you got the equation of " t2 = d2 / Vf " ? That's the only part I'm confused right now... Thank you!!