Question
Two teams of nine members each engage in a tug of war. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally. (a) What is magnitude of the acceleration of the two teams? (b) What is the tension in the section of rope between the teams?
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 4, Problem 17 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
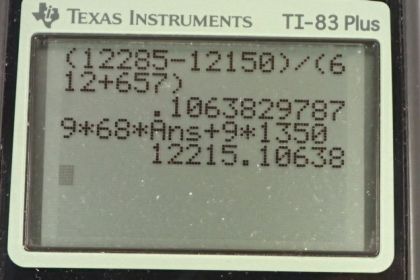
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two tug-o-war teams pulling on a rope and team B is pulling to the right and there are nine people, each exerting a force of 1365 newtons for a total force of 12,285 newtons, and there are nine people there each weighing 73 kilograms for a total mass of 657 kilograms. Then pulling the other way we have team A, each pulling with 1350 newtons, and each having a mass of 68 kilograms. So, our job is to figure out what the acceleration of this system is going to be. So, the total mass of the system is the total mass of both teams put together. We have a net force of Fb to the right, minus Fa to the left, and the net force as always equals mass times acceleration. So since F net equals this and Fnet also equals that, we can equate these two things which we do here. So mass times acceleration equals Fb minus Fa and then we'll divide both sides by m to get the acceleration. So it's the force of team B minus the total force of team A, minus the total mass of the two teams put together. So that's 12,285 newtons minus 12,150 newtons, divided by 612 kilograms plus 657 kilograms, which makes 0.106 meters per second squared. Then for part B, we're asked to find the tension in the rope and we can use one of two different perspectives to figure that out. We could use the perspective I've drawn here where we have team A exerting a force to the left and experiencing a force to the right equal to the tension force. We could have also drawn this picture F tension to the left and force of team B to the right, that would also have been fine because the force of tension is the same on each of the teams, the same magnitude anyhow, different directions. We don't need that there. So, the net force on team A which I've put a little apostrophe on it because it isn't the same net force as we were talking about up here. This net force is the net force in the entire system consisting of both teams together. This net force down here refers to the net force on just team A, and so team A experiences a tension force to the right minus the force that they're exerting to the left, and that's going to equal team A's mass times its acceleration. Team A's acceleration will be the same acceleration that we calculated in part A here. So we'll solve for Ft by adding Fa