Question
(a) An oxygen-16 ion with a mass of travels at perpendicular to a 1.20-T magnetic field, which makes it move in a circular arc with a 0.231-m radius. What positive charge is on the ion? (b) What is the ratio of this charge to the charge of an electron? (c) Discuss why the ratio found in (b) should be an integer.
Final Answer
- 3.0
- Charge is quantized in multiples of the elementary charge.
Solution video
OpenStax College Physics, Chapter 22, Problem 15 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
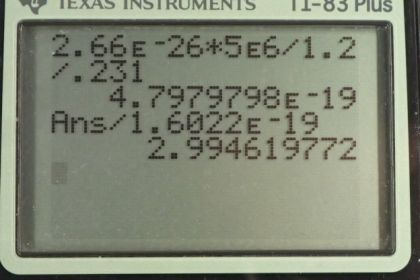
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The force due to the magnetic field on this charge is moving is qvb, the charge times its velocity times the magnetic field strength. And of course, this would have a sine theta in it, as well. But the theta is 90, we're told that the velocity and magnetic field are perpendicular and so sine of 90 is one which means we don't need to include that factor. And this magnetic field is going to be providing the centripetal force which has a formula mass times velocity squared divided by the radius of the circle. And we're going to solve for q by dividing both sides by vb. And that gives q is equals mv over B times r. So that's 2.66 times ten to the minus 26 kilograms, mass of the oxygen ion times a speed of five times ten to the six meters per second divided by magnetic field strength of 1.2 Tesla times a radius of 0.231 meters which is 4.8 times ten to the negative 19 Coulombs. Now, when we divide this number by the elementary charge of 1.6 times ten to the minus 19 Coulombs, we get 3.0 and it's no surprise that we're getting an integer when we divide the charge by the elementary charge because charge is something that is quantized, which means that it only exists in discreet numbers that are multiples of something else. So, in this case charge is a multiple of the elementary charge.