Question
When dots are placed on a page from a laser printer, they must be close enough so that you do not see the individual dots of ink. To do this, the separation of the dots must be less than Raleigh’s criterion. Take the pupil of the eye to be 3.0 mm and the distance from the paper to the eye of 35 cm; find the minimum separation of two dots such that they cannot be resolved. How many dots per inch (dpi) does this correspond to?
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 67 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
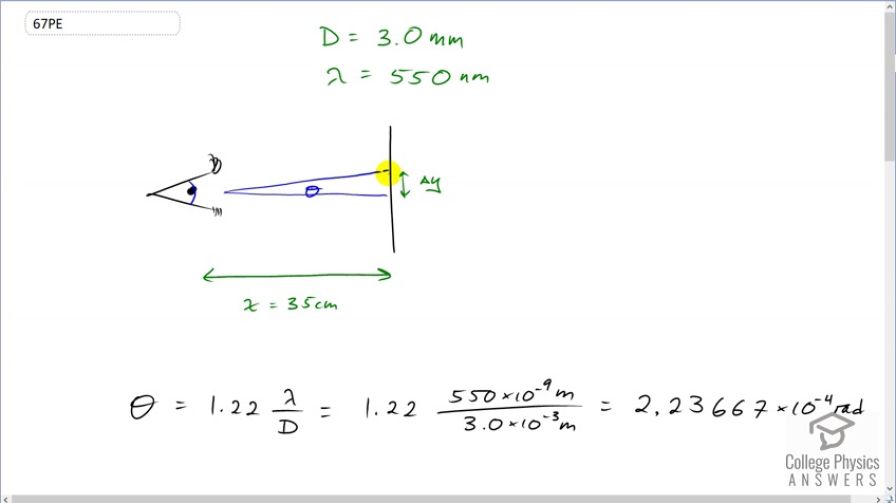
This is College Physics Answers with Shaun Dychko. Here's an eyeball with a diameter of three millimeters for the pupil and the eye is looking at two dots made by a laser printer on the page that’s 35 centimeters away. And the question is what minimum separation should be between the dots such that it's not possible to distinguish between them. And so you can't notice that there's dots and it all looks like solid lines. And so the minimum angle for that to occur is this Rayleigh criterion. And then we'll figure out what that angle is first of all and then knowing that angle and knowing how far the paper is away we'll figure out what the separation on the paper is. So the angle is going to be 1.22 times the wavelength divided by the pupil diameter. That's 1.22 times 550 times ten to the minus nine meters divided by three times ten to the minus three meters which is 2.23667 times ten to the minus four radians. And now I'm redrawing this triangle down here to figure out what this delta y is. So we'll consider a right triangle by slicing it in half. And because it's an isosceles triangle and we can take the altitude of the triangle here and it's going to intersect the base at a right angle. And this is going to be half of the base. So it's delta y over two and then this angle is going to be half of the angle that we calculated here so tangent of theta over two is going to be this delta y over two divided by x and we'll solve this for delta y by multiplying both sides by 2x and we get delta y is 2x times tangent of half the angle. That's two times 35 centimeters written as 35 times ten to the minus two meters time tangent of 2.23667 times ten to the negative four radians divided by two which is 78 micrometers and translating this into a dots per inch figure because that's the information given on the packaging for printers we have to take this one dot for every 7.8283 times ten to the minus five meters and then convert that into inches in the denominator and then we'll get dots per inch. So we multiply by one meter for every 39.3701 inches and we're left with 324 dots per inch. So if a laser printer can do 324 dots per inch or more then the eye will be unable to distinguish between the dots.