Question
Calculate the wavelength of light that has its second-order maximum at when falling on a diffraction grating that has 5000 lines per centimeter.
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 25 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
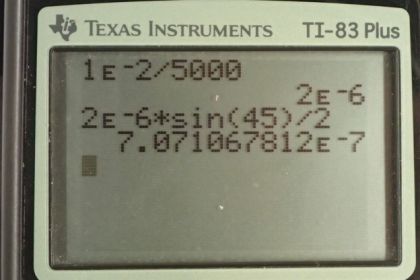
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This formula tells us where the maximum are for light going through a diffraction grating. We're given the separation between slits in the diffraction grating, the angle to the maximum, the order of the maximum m and the wavelength of the light lambda. Now we have to figure out what lambda is in this question and we're told that the angle to the second order maximum which means that m is two, is 45 degrees and the separation between slits we have to figure out given the information that there are 5,000 lines per centimeter. So we want to know how many centimeters there are between each line. And so I've written the reciprocal of the 5000 lines per centimeter here and I have one centimeter per 5000 lines and this works out to one times ten to the minus two meters for every 5,000 lines which is 2.00 times ten to the minus six meters between each line. And so that's what we're gonna substitute in for d and we'll solve this for lambda by dividing both sides by m, the order of the maximum and so lambda is d sine theta over m that's two times ten to the six meters times sine of 45 degrees divided by the order of two which is 707 nanometers must be the wavelength of the light.