Question
A telescope can be used to enlarge the diameter of a laser beam and limit diffraction spreading. The laser beam is sent through the telescope in opposite the normal direction and can then be projected onto a satellite or the Moon.
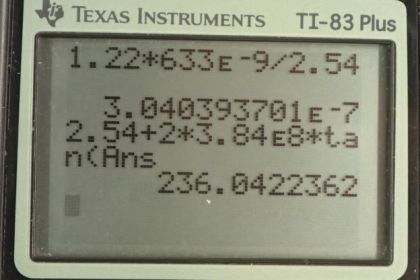
(a) If this is done with the Mount Wilson telescope, producing a 2.54-m-diameter beam of 633-nm light, what is the minimum angular spread of the beam?
(b) Neglecting atmospheric effects, what is the size of the spot this beam would make on the Moon, assuming a lunar distance of ?
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 61 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Mount Wilson telescope which has a diameter of 2.54 meters is going to be used to enlarge the laser beam being transmitted to the moon in order to reduce its diffraction spreading. So the angle with which it is spreading is given by this really criterion formula which is 1.22 times the wavelengths of light divided by diameter and we can see that as diameter increases as the size of the beam in other words the angle of diffraction spreading decreases and in part b I’ve actually drawn a picture of this diffraction spreading. So these dotted lines represent perfectly parallel rays but that's never possible because of diffraction spreading which occurs for all light beams. And this beam begins with this size capital D . And then it spreads out at this angle theta given by this formula here and it spreads out an angle theta on both sides they're all around. So and let's figure out what the angle is first of all and then we'll talk more about this picture. So it's 1.22 times the wavelength divided by the diameter. So it's 1.22 times 633 times ten to the minus nine meters divided by 2.54 meters which is 3.304 times ten to the minus seven radians. So the question in part b says, suppose this laser beam is transmitted to the moon. What would the size of the spot be on the moon. So the beam begins with the size of 2.54 meters. And if there was no diffraction spreading then the spot on the moon would be 2.54 meters here but there is diffraction spreading and we're gonna add to that this amount delta y on one side and on the other side. And so the total spot size is going to be the initial size of the beam which is D . And add to that two times delta Y. And delta Y we can figure out using this angle that we calculated in part a and it's the opposite of this triangle here delta y is the opposite of a triangle. So Tan of theta is going to be delta ydivided by x the distance to the moon which we're given as 3.84 times ten to the eight meters. So we have the total spot size is going to be the initial beam size D, size of the telescope in other words plus two times delta y and delta y can be substituted with x Tan theta . So we have 2.54 metres diameter of the telescope plus two times 3.84 times ten to the eight meters times tangent of 3.0404 times ten to the minus seven radians giving a total spot size of 236 metres for this laser beam on the moon.