Question
(a) If a single slit produces a first minimum at , at what angle is the second-order minimum? (b) What is the angle of the third-order minimum? (c) Is there a fourth-order minimum? (d) Use your answers to illustrate how the angular width of the central maximum is about twice the angular width of the next maximum (which is the angle between the first and second minima).
Final Answer
- No, there is no 4th order minimum.
- See video solution.
Solution video
OpenStax College Physics, Chapter 27, Problem 53 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
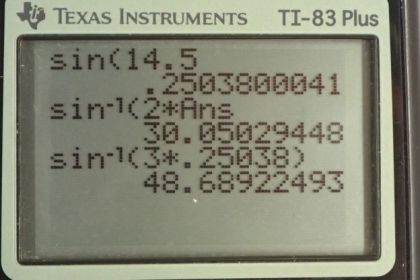
This is College Physics Answers with Shaun Dychko. We are told that the first minimum for this diffraction pattern occurs at an angle of fourteen and a half degrees. So if theta subscript one, the one meaning the first minimum and we have this formula that tells us the diffraction pattern based on the width of the slit and the wavelength of a light but neither of these pieces of information D and Lambda are given to us but we can actually deal with that because we can figure out what their ratio is because lambda over D . If you rearrange this formula we can divide both sides by mD. You end up with Lambda over D equaling sine theta over m and both theta and m we are given. So sine of fourteen and a half divided by m being one when theta is fourteen and a half gives us a ratio of 0.25038. So this is something we can substitute in place of lambda over D when we're solving for theta. So we're going to find the angle to the second minimum and so we're going to rearrange this to solve for theta divide both sides by capital D and then take the inverse sine both sides so theta is the inverse sine of m lambda over D and we have something to substitute in place of lambda over D. So down here we have theta subscript two for the second minimum is the inverse sine of m being the number two now times is ratio 0.25038 giving an angle of 30.1 degrees to the second minimum and then the third minimum will occur at inverse sine of three times that ratio 48.7 degrees and part c asks us, will a fourth minimum occur and so let's try to find the angle inverse sine of four times this number but we find that this becomes greater than one and there is no inverse sine of a number greater than one and so it's undefined and there is no fourth order minimum. Part d says compare the angular width of the first central maximum to the angular width of the next maximum and so the next maximum occurs between the minimum here and the minimum here and so we have a maximum intensity here and that's the angular width of that which I've called Alpha two that we're going to compare to the angular width this central maximum which is Alpha one, so alpha one is the angle between the borders of this central maximum and those borders are the first minimum and you decide and so that's going to be a two times theta one so this alpha one is gonna be from here to this central dotted line here which is fourteen and a half degrees and then it's going to go that many degrees again so it's twice theta one. Now theta two is going to be the difference between Alpha two I should say Alpha two is going to be the difference between theta two and theta one. So it's this here. So it's theta two minus theta one and then we're gonna compare the ratio of these two things. So Alpha one being two times theta one we're gonna divide that by Alpha two which is theta two minus theta one and see if indeed this angular width of the central maximum is twice the angular width of the next maximum. So it’s two times fourteen and a half degrees divided by 30.1 minus fourteen and a half which is approximately two. And so therefore yes the central maximum is approximately two times the angular width of the next maximum.