Question
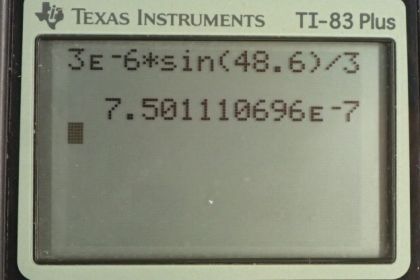
Find the wavelength of light that has its third minimum at an angle of when it falls on a single slit of width .
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're told that in the diffraction pattern for this light of some unknown wavelength that the third minimum occurs at an angle of 48.6 degrees given a slit width of three micrometers. So we have this formula for the diffraction pattern. And we're going to solve it for lambda, the wavelength. So we’ll divide both sides by m and then switch the sides around and we have the wavelength is the slit width times sine of the angle divided by the order of the minimum. So it’s three times ten to the minus six meters slit width times sine of 48.6 degrees divided by three since it's the third minimum. And that gives 750 nanometers must be the wavelength of the light.