Question
What are the three smallest non-zero thicknesses of soapy water () on Plexiglas if it appears green (constructively reflecting 520-nm light) when illuminated perpendicularly by white light? Explicitly show how you follow the steps in Problem Solving Strategies for Wave Optics.
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 75 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
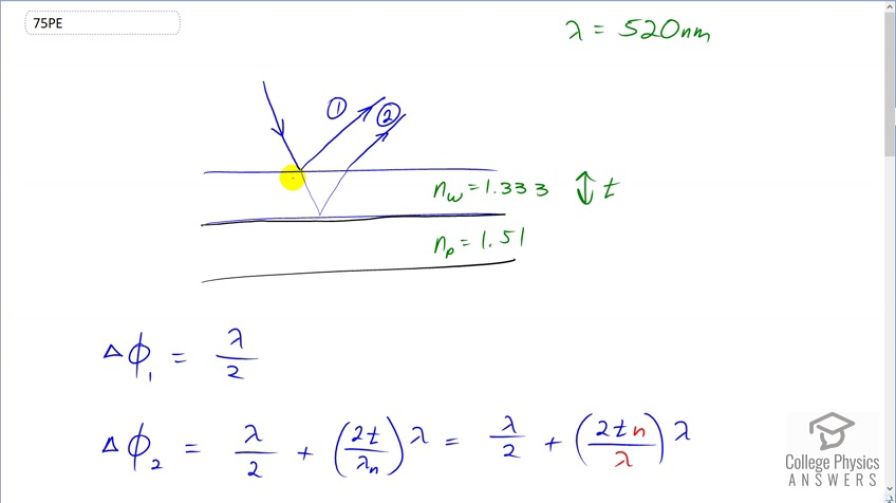
This is College Physics Answers with Shaun Dychko. Some soapy water is on top of some plexiglass and white light is incident on the soapy water and we want to find the first three thicknesses of the soapy water such that the reflection appears to be green and so it'll be green when there is constructive interference for the green wavelength of 520 nanometres between this ray one and two here. So we need to figure out what are the phase shifts for Rays one and two and then say that those phase shifts have to be a total of some integer times a wavelength and then we say that this is the wavelength. And now what should the thickness be for that. So let's figure out the phase shift for Ray one first of all. Now by the way I've drawn the picture with the ray coming in at an angle and then a reflection at an angle as well. That's only for the convenience of drawing. In actual fact the ray is perpendicular so it's coming straight in and then it's bouncing straight back as well. But I don't want to draw it that way because then you have all these rays overlapping and it's difficult to distinguish between them in the drawing. So this Ray one and two are meant to be in the same place but I’ve just drawn them so that we can see them better on an angle like this. So phase shift for Ray one is going to be half a wavelength because it's reflecting from an interface where it began in a low index of refraction material which is air index refraction of one and it's reflecting off its interface where the second medium has a higher index of refraction of 1.333 . And so when that happens there's always a phase shift of lambda over two and then for Ray two there will be a phase shift at this interface because it's beginning in the water or the soapy water material which has an index refraction of 1.333. And it's reflecting off this interface where the second medium has a higher index refraction of 1.5 this is Plexiglas. And so for the same reason as here there will be a lambda over two phase shift due to that reflection. But additionally Ray two will also have a reflection due to the additional path length I'm going through this thickness of soapy water once and then twice. And so we have to figure out how many wavelength is that additional path length and then we multiply that by Lambda to figure out how many nanometres that will, how many nanometres a phase shift that will be. So we take two times the thickness because it's traveling through that soapy material twice and divide that by the wavelength in the material that's important to notice. So this has a subscript n on it. So these do not cancel, can't do that because they're not the same number. This is lambda n which is the wavelength in the material which is the wavelength in air or vacuum divided by the index refraction of the material. Now since we're dividing by this we're going to multiply by the reciprocal of it. And so that's n over lambda which I've substituted here in place of dividing by Lambda n. Now these lambdas do cancel and so we're left with 2tn here. So that's two times the thickness of the soap film times Index refraction of the soap film. This is the phase shift for the second Ray adding to that lambda over two due to this reflection at the plexiglass interface. Constructive interference happens when the total phase shift is an integer times the wavelength. And so we're going to find the total phase shift by adding Phi 1 plus Phi 2 and substituting for each of those we have lambda over two is the phase shift for the first ray plus lambda over two plus 2tn phase shift for the second ray that has equal some integer times the wavelength. And lambda over two plus lambda over two is lambda. And so I've just rewritten that with that simplification and now we should solve for t the thickness so we subtract lambda from both sides and then afterwards divide both sides by 2n and so the thickness is n lambda minus lambda over 2n then we factor out the lambda and we get this clean formula that we can use to figure out the first three thicknesses. So the thickness is gonna be the wavelength that we want to have constructive interference four times the integer m minus one over two times indicate refraction of the soap film. So the thicknesses, where are we starting at two and not one here is 75. What are the three smallest non-zero thicknesses. If we had a one there then this would be zero. So the first three nonzero thicknesses. So we start with m equals two and minus one times 520 nanometers because that's the color green that we want to have constructive interference for divided by two times index of refraction of the soap film. And we get 195 nanometres and then we substitute three for m and then four for m doing the same calculation otherwise and we get 390 nanometers or 585 nanometers. Any of these thicknesses would cause constructive interference with the color green, when soap film is on Plexiglas.

