Question
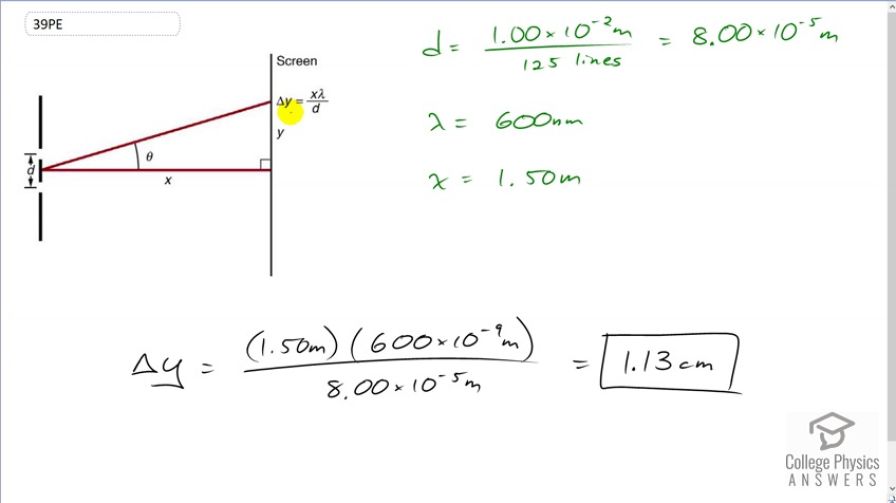
The analysis shown in the figure below also applies to diffraction gratings with lines separated by a distance . What is the distance between fringes produced by a diffraction grating having 125 lines per centimeter for 600-nm light, if the screen is 1.50 m away?

Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When theta is really small, we can say that this distance Delta y the separation between fringes is going to be x the distance from the screen to the slits or the diffraction grating times the wavelength divided by d, this distance between each line in the diffraction grating. So we're told that there are 125 lines per centimeter in this diffraction grating but we need to turn this into meters between each line and so we'll take the reciprocal of that number we’re given and we'll say it's one centimeter written as times ten to the minus two meters divided by 125 lines giving us 8.00 times ten to the minus five meters between each line and the wavelength we’re told is 600 nanometers and the distance between the screen and the diffraction grating is one and a half meters. And so that means the distance between the bright fringes is going to be one and a half meters times 600 times ten to the minus nine meters wavelength divided by eight times ten to the minus five meters separation between the slits and that is 1.13 centimeters.
