Question
How many lines per centimeter are there on a diffraction grating that gives a first-order maximum for 470-nm blue light at an angle of ?
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 23 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
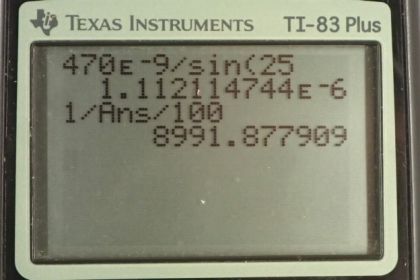
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have this formula for the fringes of constructive interference due to a diffraction grating. And this formula will tell us d the separation between lines in the diffraction grating and then we'll use that to figure out the number of lines per centimeter. We're told that the first order bright interference fringe occurs at an angle of 25 degrees given light with a wavelength of 470 nanometers. So we'll solve this ford by dividing both sides by sine theta and we get d is m lambda over sine theta. So the order is one and we substitute 470 times ten to the minus nine meters for the wavelength divided by sine of 25 degrees giving us 1.11211 times ten to the minus six meters per line. So this is the separation between each line. Now we want lines per centimeter to answer the question. So we have one line for every this many meters and then we multiply by one meter for every hundred centimeters to cancel the meters and we're left with lines per centimeter. And this works out to 8990 lines per centimeter.