Question
If a polarizing filter reduces the intensity of polarized light to 50.0% of its original value, by how much are the electric and magnetic fields reduced?
Final Answer
The electric and magnetic fields are each reduced by a factor of 0.707.
Solution video
OpenStax College Physics, Chapter 27, Problem 98 (Problems & Exercises)
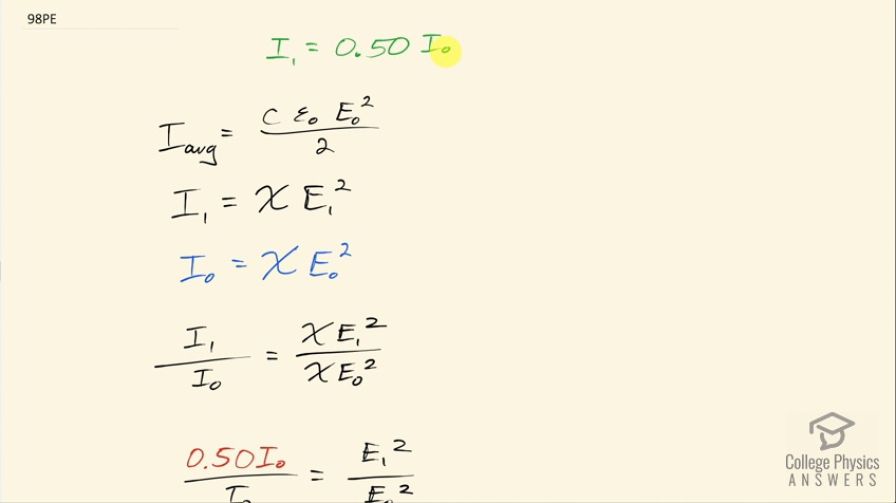
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The intensity of light after traveling through a polarizing filter is half of what it was initially and we are asked to figure out how does this mean... so we are asked to figure out in what way does the electric and magnetic fields change? Well, the average intensity is the speed of light times permittivity of free space times the peak electric field squared over 2 but all of this stuff here— these constants can be summarized by just some letter x suppose— so the intensity after passing through the polarizing filter is some constant x times the electric field strength squared and I am labeling this after the polarizing filter with the subscripts 1 and before the polarizing filter, let's call that the original intensity I naught equals the same constants times the electric field before the polarizing filter, which we'll call E naught squared. So when we divide these two intensities, we are going X times E 1 squared over XE naught squared and we can replace I 1 after the polarizing filter with 0.50 times I naught and so the I naught's cancel and we can rearrange a little bit by multiplying both sides by the electric field originally squared and we have E 1 squared equals 0.50 times E naught squared and then take the square root of both sides and we have E 1 is the square root of 0.50 times E naught. So this means the electric field after passing through the polarizing filter is 0.707 times the electric field before the polarizing filter. Now there's another formula for the average intensity in terms of the magnetic field strength and that's speed of light times the magnetic field squared divided by 2 times the permeability of free space and the logic is the same so ... we can say B 1 will be 0.707 times B naught as well. So the electric and magnetic fields are both reduced by a factor of 0.707.
