Question
To save money on making military aircraft invisible to radar, an inventor decides to coat them with a non-reflective material having an index of refraction of 1.20, which is between that of air and the surface of the plane. This, he reasons, should be much cheaper than designing Stealth bombers. (a) What thickness should the coating be to inhibit the reflection of 4.00-cm wavelength radar? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- This is quite a thick layer and would be expensive to make consistently thick everywhere. It would also add significant weight.
- This idea is unrealistic, and even in the best case scenario where it isn't too expensive or heavy it would defend against only one frequency of radar. An easy countermeasure would be to use a different radar frequency.
Solution video
OpenStax College Physics, Chapter 27, Problem 83 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
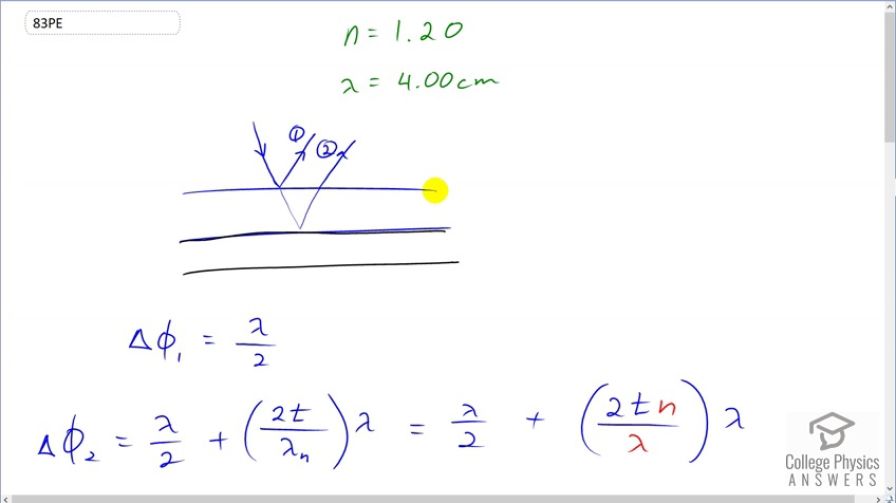
This is College Physics Answers with Shaun Dychko. An inventor has an idea of coating military aircraft with some layer of material here that would have destructive interference for Radar and by doing that it will make the airplane invisible in the Radar because the rays would not reflect back to receiver. So, here are some incident Radar rays and there's going to be reflection from the first part of the surface that is in contact with the air and that will be ray one that gets reflected and that will have some phase shift due to this reflection since it’s going from a material with low index of refraction which is air 1.0 into a material with a high index of refraction which we are told is 1.2 and so reflecting from interface between low index to high index results in automatic phase shift of pi over two… or lambda over two, so half a wavelength and then ray two, on the other hand, will travel through the material and then bounce off this interface with the surface of aircraft and then have a phase shift due both to an automatic lambda over two phase shift due to this reflection because this is going from a material with index of refraction 1.2 to a material with very high index of refraction, it doesn’t even transmit the rays. I mean this is metal here. and this reflection is going to have a lambda over two phase shift due to reflection and then additionally there will be a phase shift due to this additional path length traveled by ray two and the total phase shift between these two rays has to be some integer plus a half times a wavelength in order for destructive interference to occur. So, let's figure out what is delta phi two as a phase shift for ray two. So, we said that its lambda over two due to the reflection and then we add to that some number of wavelengths traveled multiplied by the wavelength in air and then we will figure out what the phase shift is due to the path length difference. So, this is two times the thickness because its traveling once down through the material and then up again back up, so its traveling through the material twice. And then we are dividing by lambda over n and lambda over n or lambda subscript ‘n’ I should say is lambda over n and then when we dividing by this we are going to instead multiply by its reciprocal. So, we have lambda over two plus two times thickness times index of refraction of the material divided by the wavelength in air times the wavelength in air and these cancel, leaving us with two t n for that term and so the phase shift of ray two is lambda over two plus two t n. So, we add the two phase shifts together and this has to be some integer plus a half times wavelength in order to have destructive interference and we are gonna solve this for t. So, lambda over two plus lambda over two is lambda and then I distributed the lambda on this side into the brackets. So, we have lambda m plus lambda over two and then subtract lambda from both sides and then lambda over two minus lambda is same as lambda over two minus two lambda over two to get a common denominator there, and this makes negative lambda over two. And then we will divide both sides by two n in order to get the… an expression for the thickness. Okay. So, the thickness is lambda times two m minus one over four n where I made the… What did I do here? So, this has to be written over two to have a common denominator. So, that’s two lambda m over two and then factor the lambda out there and you have a lambda times two m minus one all over two and then we are dividing by two n here, so that’s times one over two n and that’s where the… denominator four n comes from. Okay. Good enough. So, plug in numbers. We have a four centimeters wavelength for the radar times two times, we’ll choose m to be one, so we will get the minimum possible thickness that will result in destructive interference, minus one divide by four times the index of refraction of 1.2 which is a thickness of 0.833 centimeters. Well, this is actually quite thick and it will be very difficult to make the layer consistently thick over the surface of a very large military aircraft. So that’s one problem, it’ll be expensive to be that precise and secondly this much material painted on to the aircraft will make it heavier and that’s important problem for aircraft. They take great pains to make the aircraft as light as possible in order to have a greater speed as well reduce fuel cost. So, this idea is unrealistic for those reasons plus even if it did work, it would defend only against one frequency of radar. There is nothing stopping the enemy from choosing a slightly different wavelength which would still work, in which case, a different wavelength would work for the radar detecting purposes, but it would not be destructively interfered by this thickness of layer. So, this idea does not work for many reasons.
