Question
Find the minimum thickness of a soap bubble that appears red when illuminated by white light perpendicular to its surface. Take the wavelength to be 680 nm, and assume the same index of refraction as water.
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 73 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
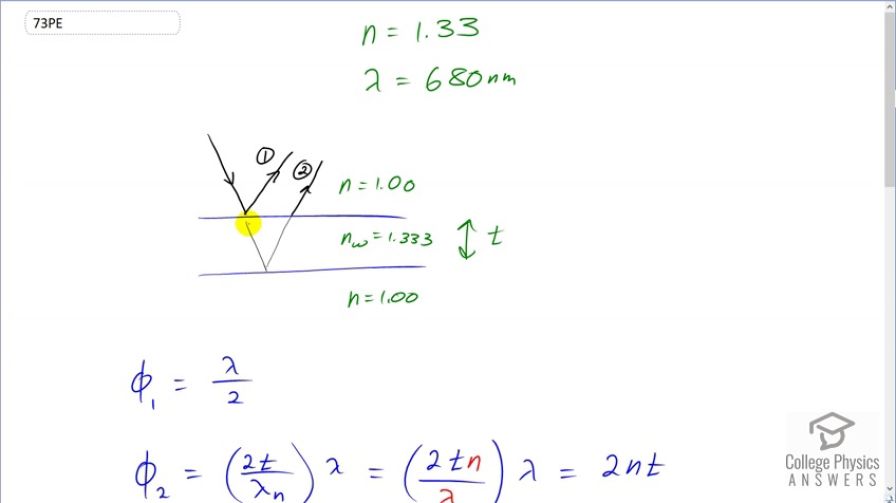
This is College Physics Answers with Shaun Dychko. In order for this soap bubble to appear red when it's illuminated by white light. We need to have the red color experience constructive interference when there's reflection for these two rays, as ray number one occurs from a reflection on the outside of the soap bubble and Ray two is due to reflection from the inside of the soap bubble and each of these rays is going to experience a phase shift and when the phase shift is such that the total phase shift is some integer times the wavelength then there will be constructive interference and we'll figure out what thickness the soap bubbles should be such that the color red of 680 nanometres experience is the constructive interference. We're told the soap bubble has an index refraction the same as water which is 1.333. Now I've written n equals one on the bottom here because this is air at this in this position because this soap bubble has air on the inside and so this is the outside where n is one and the white light as incident and it's reflecting from this interface and it's reflecting from interface where the second medium is of a higher index of refraction 1.33 and the beginning in an index of 1.0 . And so this reflection causes a phase shift of lambda over two. So our job right now is to figure out what is the phase shift in nanometers for each of these rays and into a four number one, it's lambda over two. Now the phase shift for Ray two is going to be the number of extra wavelengths that this Ray has travelled due to going through this additional distance once through the thickness and then a second time and that's going to be two times the thickness because it does a round trip it goes once twice. So it's travelling that thickness twice and we want to figure out how many lambdas that is and then multiply that by Lambda but these lambda is not the same. This one here has a subscript n because this is the wavelength in the material. So this is the wavelength in the water and lambda in the material is the wavelength in a vacuum or in air because air is essentially in this refraction of a vacuum of one and so lambda n is lambda over the next refraction. Now since we're dividing by this thing we're gonna multiply by the reciprocal of that. So we have two times thickness times Index refraction of the soap material which is that of water divided by lambda and then we multiply that by Lambda. So this is the number of lambdas multiplied by Lambda giving us the number of nanometres of phase shift. So two and t is their phase shift for ray two and there is no phase shift as a result of this reflection by the way because this ray is starting in a material with an index refraction of 1.3 and then reflecting off this interface where the second medium has a lower index refraction and when refraction occurs in that circumstance the reflected ray does not have a phase shift resulting from the reflection. So there is a phase shift here due to reflection because it's starting in low and reflecting from a material that has high index refraction. But here no effect or no phase shifted due to reflection. Now constructive interference happens when the total phase shift is some integer times the wavelength and so we'll add the phase shifts of Ray one plus the phase shift of Ray two it has to equal that and we substitute for each to these. So we have lambda over two as the phase shift of Ray one that reflected off the top of the soap bubble and then two times index refraction of water times the thickness of the soap bubble is a phase shift for Ray two and that's meant to equal some integer times lambda. Now we know what the wavelength is that we want to have constructive interference 680 nanometres color red and we want to solve for t . So first of all we're going to get rid of fractions by multiplying everything by two. So we have lambda plus 4nt equals 2m lambda and then we'll subtract lambda from both sides. And afterwards we will divide both sides by 4m and then we have thickness is 2m lambda minus lambda over 4m and then we can factor out the Lambda and we get a nice clean formula lambda times 2m minus one over 4n and now we can choose different values for m. There are many different thicknesses that will have constructive interference for this particular color and we're going to be choosing the minimum thickness we're told and so we want to take the minimum m which is one. So we put in the number one for m that we have 680 nanometres times two times one minus one all over four times the index of refraction of water 1.333 which is 128 nanometres. That's the minimum thickness of the soap film in order to have it appear red when illuminated by white light.
