Question
(a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of , at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?
Final Answer
- 5
Solution video
OpenStax College Physics, Chapter 27, Problem 17 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
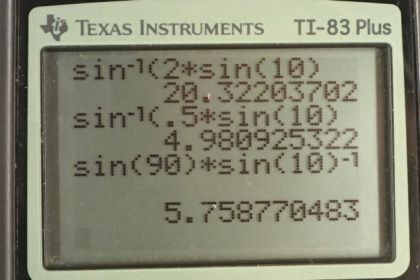
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're told that the first order maximum for light falling on a double slit occurs in an angle of 10 degrees. Now, we don't know what the wavelength is nor do we know the separation between the slits D but we do know this Theta and this M. So, we can figure out a lot from that anyway. Part A asks us to find the angle to the second order maximum. Now, we can rearrange this to solve for sine Theta and divide both sides by D and we get that sine Theta is the order times the wavelength divided by the separation between slits. And then, we can take the inverse sine of both sides to find Theta but we don't know Lambda nor D. But, we do know their ratio because we could rearrange this formula again and then in blue, I've written Lambda divided by D. So, Lambda divided by D you get by multiplying both sides by one over M D. And, we get sine Theta over M on one side and you get Lambda over D on the other. And so, based on this ten degrees that we're told for the first order maximum, we can substitute for Theta and M and find that the ratio wavelength divided by separation between slits, Lambda over D, is sine of ten divided by one, which is just sine of ten. So, we're going to substitute for Lambda over D with sine of ten to find Theta. So, Theta's going to be the inverse sine of two because we're told that this is the second order maximum we're concerned with so M is two times sine of ten. And, this works out to 20.3 degrees. So, that's the angle to the second order maximum. Part B asks for the angle to the first minimum, and the choice of words is a bit confusing because that means that M is the number zero. They did not say first order minimum. If they had said first order minimum, then M would be one but they just said the first minimum, which will occur when M is zero. So, we'll divide both sides by D here and we get that sine of the angle is M plus a half, which is what you have when you're looking for minima, times Lambda over D. And Lambda over D, we've already discussed, is sine of ten. And so, the angle then is the inverse sine of M plus a half times sine of ten. So, M is zero and then add a half to that, multiply by sine of ten, then take the inverse sine of that product and you get 4.98 degrees. That's the angle to the first minimum. And then, part C asks us for the highest possible order maximum and that will occur when Theta is 90 degrees because if you consider these two slits and light is falling on this screen over here, the largest angle you can possibly have is going to be 90 degrees and at precisely 90 degrees, in fact, you'll get no maximum at all because light will be parallel to the screen. But, 90 degrees is that threshold between possible and not possible. So, we're going to take Theta to be 90. So, we're going to solve for M then and divide both sides by Lambda here. So, the order is going to be separation between slits times sine of Theta divided by Lambda and Theta, we know, is 90 and D over Lambda is the reciprocal of Lambda over D and Lambda over D, we already know, is sine of ten. So, we're going to take the reciprocal of sine of ten here. So, sine of 90 times sine of ten gives, both to the negative one by the way, gives 5.76. Now, the number M has to be an integer and we always have to round down. And so, five is going to be our answer even though this would normally round to six. Anything greater than 5.76 will give an angle greater than 90, which doesn't make any sense. And so, we have to take the closest integer that is less than this number, which is five.