Question
Suppose you put on two pairs of Polaroid sunglasses with their axes at an angle of . How much longer will it take the light to deposit a given amount of energy in your eye compared with a single pair of sunglasses? Assume the lenses are clear except for their polarizing characteristics.
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 99 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
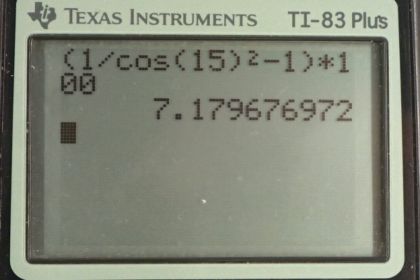
Calculator Screenshots
Video Transcript
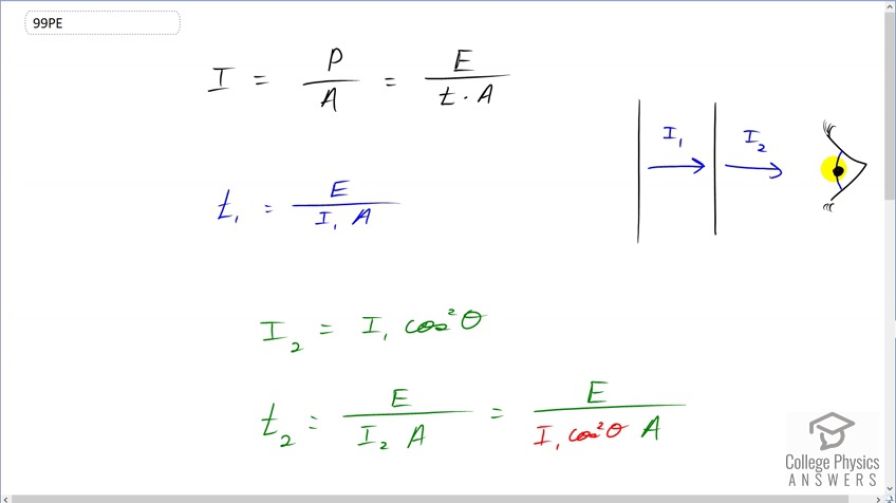
This is College Physics Answers with Shaun Dychko. We're going to see how much longer it takes for a given amount of energy to be deposited into the eye, if you have two pairs of sunglasses where the second pair is, has a polarization axis that is 15 degrees different from the polarization axis of the first pair of sunglasses. So, there'll be some amount of time needed to deposit a given amount of energy, E, into the eye, and we can figure that out based on the definition of intensity. It's the power per area and power is energy per time, is the rate at which energy is produced or deposited and so on. And so we can solve this for t by multiplying both sides by t and so we get t is, and dividing both sides by I as well. So, we get t is energy divided by intensity times area. So, t one the amount of time for this given amount of energy to be deposited with only one pair of sunglasses is going to be E divided by intensity one times A and the E does not get a subscript because the amount of energy deposited is the same in both scenarios. It's the time that's different which is why the t does have a subscript one here and the intensity also is different which is why I get the subscript one and the area is the same. So, now when we have the two sunglasses here there's some final intensity I two which is I one multiplied by cosine of the angle between the polarization axes squared. And we can write down t two is the amount of energy deposited divided by intensity two times area and then replace I two with I one cos squared theta and then the percent increase in time then is the difference between t two and t one divided by t one times 100% or t two over t one minus one times a 100. So, I write down t two which is E over I one cos squared theta a and then divide by t one is the same as multiplying by its reciprocal. So the reciprocal is going to be I one A over E. So, I have written that here I one A over E and then a bunch of things cancel which is nice and we're left with one over cos square theta minus one times 100%. So that's one over cos squared of 15 minus one times 100% which means the time will be 7.2% greater when you have the two pairs of sunglasses.