Question
Show that if you have three polarizing filters, with the second at an angle of to the first and the third at an angle of to the first, the intensity of light passed by the first will be reduced to of its value. (This is in contrast to having only the first and third, which reduces the intensity to zero, so that placing the second between them increases the intensity of the transmitted light.)
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 27, Problem 89 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
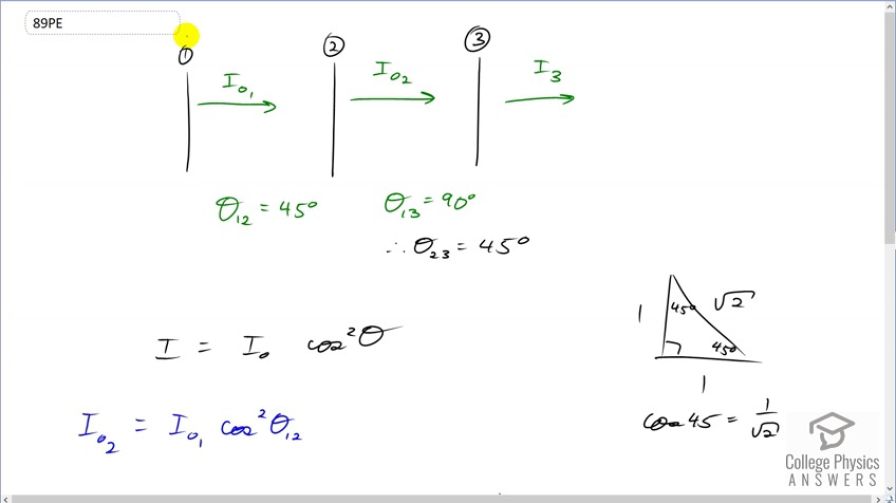
This is College Physics Answers with Shaun Dychko. We have three polarizing films and the polarization axis of film three is 90 degrees to that of film one. And without this film two in between them that would result in no intensity being transmitted at all. But it turns out that, interestingly, if we put a filter in between them, polarizing filter here between number one and three, then we will have some intensity getting transmitted because film two shifts the polarization axis of this light to some other angle here, and which then is not at 90 degrees to film three and so some of it does get transmitted. And the question here is, we're going to show that the transmitted final intensity will be 25% of this here. So, we're going to show that I three is 25% of I naught one. So, the final intensity transmitted is going to be 25% of whatever got through the polarization film number one. Okay. So, the angle between the polarization axes of film two and one is 45 degrees, we're told, and the angle between one and three is 90. And that means that the angle between two and three must be 45. So the transmitted intensity by any polarizing film equals the incident intensity times cosine of the angle between their polarization axes squared. And so I naught two, this intensity transmitted through film two, is going to be I naught one multiplied by cosine of the angle between the axes of two and one squared. And intensity three, which is our final intensity, is going to be intensity passed through film two times cosine of the angle between the polarization axes of film two and three squared. Now I naught two, we just have found an expression for it is this, so we'll substitute that in here, and then we can divide both sides by I naught one and then this is what we're trying to answer what is, you know, show that the I three overI naught one is 25% and it equals cosine theta one two squared times cosine theta two three squared. So, that's cosine of 45 squared times cosine of 45 squared and cosine of 45, if we use a special triangle, we can see that it is adjacent of a hypotenuse which is one over root two. So, we have one over root two squared times one over root two squared. So that's one-half times a half which is a quarter which is 0.25 and so therefore we have shown that the transmitted intensity through film three is 25% of what went through film one.
