Question
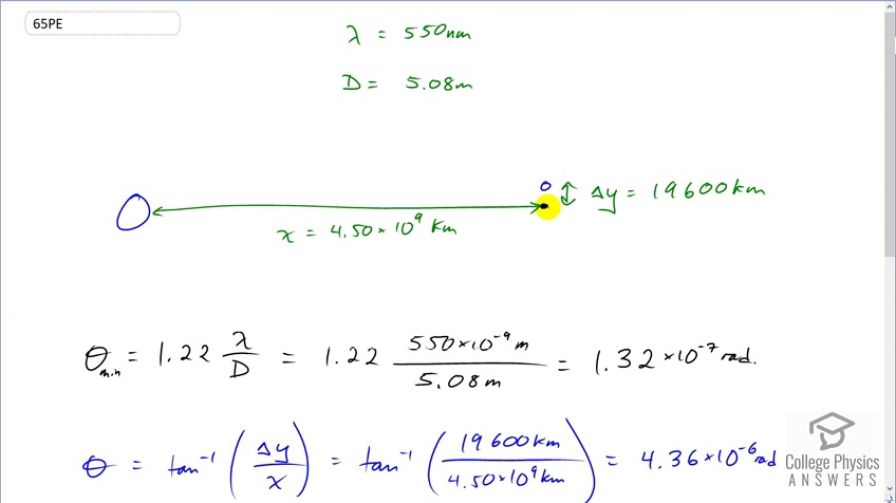
(a) The planet Pluto and its Moon Charon are separated by 19,600 km. Neglecting atmospheric effects, should the 5.08-m-diameter Mount Palomar telescope be able to resolve these bodies when they are from Earth? Assume an average wavelength of 550 nm. (b) In actuality, it is just barely possible to discern that Pluto and Charon are separate bodies using an Earth-based telescope. What are the reasons for this?
Final Answer
- . Therefore, yes, the Mount Palomar telescope will be able to observe Pluto's moon Charon.
- Aberrations by the atmosphere are significant.
Solution video
OpenStax College Physics, Chapter 27, Problem 65 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The planet Pluto and its moon Charon are separated by 19600 kilometers. And the question here is based on diffraction effects. is it possible for the Mount Palomar telescope on Earth to distinguish between Pluto and its moon and we're told that the wavelength it observes with is about 550 nanometres and the diameter of the telescope is 5.08 meters. And Pluto is 4.5 ten to the 9 kilometers away. So the minimum angle based on the Rayleigh criterion is 1.22 times lambda over D . So these two things need to be separated by this angle here theta minimum, so it’s 1.22 times 550 times ten to the minus nine meters divided by 5.08 meter diameter of the telescope which is 1.32 times ten to the minus seven radians and so let's figure out what this angle actually is based on the geometry here and it's going to be the inverse tangent of this opposite 19600 kilometers divided by the adjacent 4.5 times ten to the nine kilometers which is 4.36 times ten to the minus six radians. And so this angle is greater than the minimum needed. And so yes it will be possible for the Mount Palomar telescope to observe Pluto's moon Charon but it turns out that it can't from the earth because of aberrations caused by the atmosphere. And however a Hubble telescope would not be affected by the atmosphere and the Hubble telescope could observe this moon. If the Hubble telescope has the same diameter mirror.
