Question
At what angle does a diffraction grating produces a second-order maximum for light having a first-order maximum at ?
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 33 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
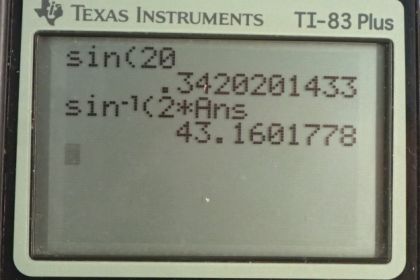
This is College Physics Answers with Shaun Dychko. We're told that a first order maximum for whatever wavelength this is, occurs at 20 degrees. And the question is where will the second order maximum be? Well this formula will help us find it and we need to know what the separation is between the slits in the diffraction grating and the wavelength. But we're given neither of these pieces of information. But it turns out that we can deal with that by just finding their ratio because we do know the order and the angle. And so we can say that the angle that we want for the second order is going to be the inverse sine of the order m which is going to be two times lambda over d. So if we knew what lambda over d was, we could substitute that in. And it doesn't matter what lambda is or what d is, what matters is what the ratio is. And so we can solve this for lambda over d by dividing both sides by md. And then we find that lambda over d is sine theta over m and we're given information for the first order maximum. So that sine of 20 degrees divided by one which is 0.34202. So this is what lambda divided by d is. And so we can plug in 0.34202 in place of lambda over d multiplied by the second order number which is two, take the inverse sine of that and we get an angle of 43.2 degrees to the second order maximum.