Question
Suppose you have a 9.00 V battery, a capacitor, and a capacitor. (a) Find the charge and energy
stored if the capacitors are connected to the battery in series. (b) Do the same for a parallel connection.
Final Answer
- ,
- ,
Solution video
OpenStax College Physics, Chapter 19, Problem 66 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
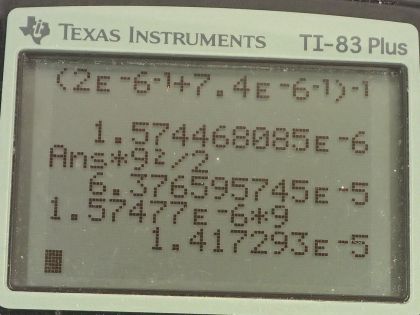
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Given a 9.00 volt battery, a first capacitor with capacitance 2.00 microfarads and a second capacitor with capacitance 7.40 microfarads, the question is to figure out the energy stored in the system of capacitors and the total charge stored on them given a series connection in part (a) and then a parallel connection in part (b). So our first step is to figure out the total equivalent capacitance and for series, it's 1 over the first capacitor plus 1 over the second capacitor always to the power of negative 1. And so we have 1 over 2.00 microfarads plus 1 over 7.40 microfarads written as times 10 to the minus 6 in each case and then raise that sum to the exponent negative 1— which is a way of flipping the number that you get in the middle here— and you get 1.57447 times 10 to the minus 6 farads and we are keeping lots of digits in this figure because it's an intermediate calculation, we only do rounding in the final answer. So the energy will be this equivalent capacitance multiplied by the voltage squared divided by 2 and that's 6.38 times 10 to the minus 5 joules. Capacitance is defined as the amount of charge stored divided by the voltage required to put that charge on the capacitor. So we can solve this for Q by multiplying both sides by V and the charge then is the capacitance times the voltage. So that's 1.57477 times 10 to the minus 6 farads times 9.00 volts which is 1.42 times 10 to the minus 5 coulombs. In part (b), the total equivalent capacitance will be the direct sum of the two capacitance's because that's the way to add capacitance in parallel. So that's 2.00 microfarads plus 7.40 microfarads which is 9.40 times 10 to the minus 6 farads. Let me use the same formulas to calculate the energy and charge as we did in part (a). So the energy is capacitance times voltage squared divided by 2 so that's 9.40 times 10 to the minus 6 farads times 9.00 volts squared divided by 2 which is 3.81 times 10 to the minus 4 joules. And the total charge stored on the two capacitors will be 9.40 times 10 to the minus 6 farads times 9.00 volts which is 8.46 times 10 to the minus 5 coulombs.