Question
A nervous physicist worries that the two metal shelves of his wood frame bookcase might obtain a high voltage if charged by static electricity, perhaps produced by friction. (a) What is the capacitance of the empty shelves if they have
area and are 0.200 m apart? (b) What is the
voltage between them if opposite charges of magnitude 2.00 nC are placed on them? (c) To show that this voltage poses a small hazard, calculate the energy stored.
Final Answer
Solution video
OpenStax College Physics, Chapter 19, Problem 67 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
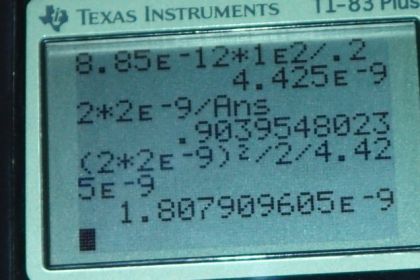
This is College Physics Answers with Shaun Dychko. The bookshelf of this nervous physicist is described as a wooden bookshelf in order to avoid conducting charges between the metal shelves. And so, the metal shelves can serve as plates of parallel plate capacitors. Now, the capacitance of these two middle shelves is going to be the permittivity of free space times the area of the shelf divided by the separation between them. And so, we have 8.85 times ten to the minus 12 farads per meter, times the area of one shelf, which is 100 square meters, divided by 0.200 meters of separation between them, giving a capacitance of 4.43 times ten to the minus nine farads, or 4.43 nanoFarads. And, the next question is: What's the voltage between the shelves if opposite charges of equal magnitude are placed on adjacent shelves? So, that means, the top shelf, say will have positive two nanoCoulombs, and the opposite charge of equal magnitude will be placed on the other shelf, and so we have negative two nanoCoulombs on the other shelf. And, that makes a charge difference between these shelves of a total of 4 nanoCoulombs because two minus negative two makes four. And so, in this formula here, where we have capacitance equals the charge divided by the voltage, we can solve for V by multiplying both sides by V over C. And, we end up with V equals Q over C, and this Q is going to be two times two nanoCoulombs, for a total of four. So, four nanoCoulombs divided by 4.425 nanoFarads gives 0.904 volts. And then, the energy stored in this parallel plate capacitor is going to be the charge squared divided by two times the capacitance. I could have used this voltage, and I could have done capacitance times voltage squared over two, that would have been fine, but I prefer not to use some numbers that I've calculated just in case my calculation was wrong, that would make the result from this formula also wrong. And so, I'm using numbers given to us directly in the question, which is the charge. And, I have no choice but to use this capacitance. Although, I suppose I could plug in the formula for capacitance if I wanted to use the raw numbers, but this is good enough for me. So, we have charge squared, which is two times two nanoCoulombs, and we square that result and divide by two, and also divide by the capacitance that we calculated in part A, and this gives 1.81 times ten to the minus nine Joules, and that is a very harmless amount of energy, and this is a harmless amount of voltage. So, the nervous physicist has no reason to be nervous.