OpenStax College Physics, Chapter 19, Problem 3 (Problems & Exercises)

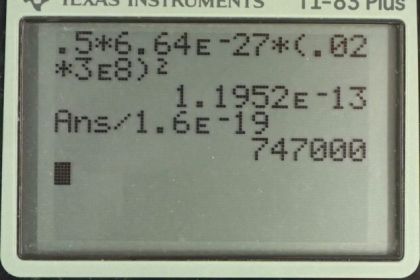
This is College Physics Answers with Shaun Dychko. The kinetic energy of this bare helium nucleus is one half times its mass times its speed squared. So, that's one-half times mass times 0.02 times C, which is the speed of light squared. We're told that this thing is traveling at two percent the speed of light and 0.02 is two percent written as a decimal. So, we have one-half times the mass of the bare helium nucleus, 6.64 times ten to the minus 27 kilograms times 0.02 times 3.0 times ten to the eight meters per second, and we square that product. And, we end up with 1.20 times ten to the minus 13 Joules as the kinetic energy. And, we're asked to convert this into electron volts because this seems like a very small number because it's times ten to the minus 13. And, this is the reason why electron volts were invented in order to make numbers easier to write when you're talking about small atomic particles. So, we can instead write this as 1.1952 times ten to the minus 13 Joules, where I've written this unrounded, in order to avoid intermediate rounding error. And, we multiply by this conversion factor of one electron volts of energy for every 1.60 times ten to the minus 19 Joules of energy. The Joules cancel, leaving us with electron volts, and that is 7.47 times ten to the five electron volts. Now, the next question is, through what voltage would this particle have to be accelerated starting from rest in order to reach this final velocity here, two percent C. So, the change in potential energy is the charge multiplied by the potential difference. And, we know that this equals the change in kinetic energy. There's a negative sign there because the change in kinetic energy is opposite to the change in potential energy, but the negative sign's not really that important in this question, because it's giving us a speed and it's not really clear which direction negative would really mean. But, anyway, I included it there. So, that's negative of one-half mass V final squared minus one-half mass the initial squared, and there's no initial speed, we assume, and so that term is zero. And, that means, Q V equals negative one-half M Vf squared. So, that's one-half M 0.02 times C squared and then we can divide both sides by Q because we want to solve for V, the potential difference. So, the potential difference is negative mass times 0.02 C squared divided by two times the charge. So, that's negative of 6.64 times ten to the minus 27 kilograms mass of V bare helium nucleus, times 0.02 times three times ten to the eight meters per second, all squared, divided by two times two, don't forget that two there. This is because helium nucleus has two protons, and so the charge is going to be two times the elementary charge. So, that's two times 1.60 times ten to the minus 19 Coulombs. And, we end up with negative 3.74 times ten to the five volts would be the potential difference through which the bare helium nucleus would need to be accelerated starting from rest such that it reaches the speed of two percent the speed of light.