Question
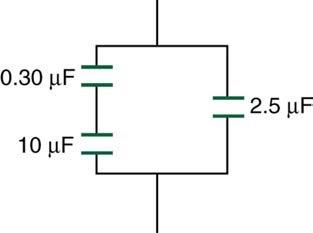
Find the total capacitance of the combination of capacitors shown in Figure 19.33.
Final Answer
Solution video
OpenStax College Physics, Chapter 19, Problem 60 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job in this question is to imagine that all three of these capacitors are written as only one capacitor, what would that one capacitance be such that it would have that same capacitance as the three of these combined as shown. So we will answer that by first redrawing the circuit as this circuit here where the left hand branch is replaced with a single capacitor with the capacitance equivalent to these two—C 1 and C 2—combined together and I don't say 'added together' because they don't strictly add; since they are in series, it is actually the reciprocals that are going to add. And then with these two capacitors in parallel, this being a real physical capacitor C 3 and this one on the left being a hypothetical capacitor, which would be the same capacitance as these two real capacitor's combined. We add these together to make a make a total capacitance to answer our question. Okay! So first step is figuring out what is this first equivalent capacitance of C 1 and C 2 together. Now when capacitors are in series— as these are— the total capacitance is going to be the reciprocal of the sum of the reciprocals of each capacitor. So we take the reciprocal of capacitor 1 and so that's 1 over C 1 and add that to the reciprocal of capacitance two, find that sum then take the reciprocal of that sum and that will be our equivalent capacitance. And I found a common denominator here so multiply this fraction by C 2 over C 2 and this fraction by C 1 over C 1 and so the denominator C 1 multiplied by C 2 and on top we have C 2 plus C 1 and then taking the reciprocal of that is straightforward since we now have a single fraction and we just flip it and so it is C 1C 2 over C 1 plus C 2— that is this equivalent capacitance number one, C eq 1. Then these capacitors are in parallel and so that means their equivalent capacitance will be the direct sum of these two capacitances. So in parallel, we add this first equivalent capacitance plus capacitance C 3. We replace C eq 1 with C 1C 2 over C 1 plus C 2 and add to that C 3 and now we plug in numbers. So C 1 is 0.30 microfarads and C 2 is 10 microfarads, take the product of those and divide by their sum and then add to that 2.5 microfarads then we end up with 2.79 microfarads. So if this whole circuit was replaced with one single capacitor with the same capacitance in total, it would have capacitance of 2.79 microfarads.
