Question
An evacuated tube uses an accelerating voltage of 40 kV to accelerate electrons to hit a copper plate and produce x rays. Non-relativistically, what would be the maximum speed of these electrons?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

1×108 m/s1\times 10^{8}\textrm{ m/s}

Solution video

OpenStax College Physics, Chapter 19, Problem 2 (Problems & Exercises)

OpenStax College Physics Answers, Chapter 19, Problem 2 video poster image.

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

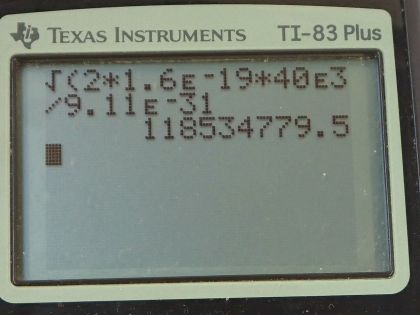
Calculator Screenshots

  • OpenStax College Physics, Chapter 19, Problem 2 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. Electrons are accelerated through a potential difference of 40.0 kilovolts which is 40 times 10 to the 3 volts and the question is what would their maximum speed be ignoring any relativistic effects? So the change in potential energy of these electrons is the charge multiplied by the potential difference and the amount of change in kinetic energy of the electrons equals the amount of change in potential energy. and I put absolute value bars in here just that so we can ignore negative signs here and we'll say that the kinetic energy is equal to the magnitude of the potential energy change. So the change in kinetic energy is one-half times mass times final velocity squared because there is no initial velocity because they are accelerated from rest so I didn't write that term down. And we can solve for v f squared by multiplying both sides by 2 over m and we get v f squared is 2qΔV over m and then take the square root of both sides to solve for the final speed. So that's the square root of 2 times the charge times the potential difference divided by mass of an electron. So that's 2 times 1.60 times 10 to the minus 19 coulombs times 40 kilovolts divided by 9.11 times 10 to the minus 31 kilograms— mass of an electron— square root all of that and you get a speed of 1. or well... I didn't put in any point at all, I just put one significant figure because this 40 kilovolts it's a bit ambiguous as to how many significant figures it has and it's probably fair to assume it has only one. So 1 times 10 to the 8 meters per second would be the maximum final speed of these electrons.

Comments

Submitted by qea on Mon, 01/02/2023 - 20:27

link

i came here to see how many electrons should i take. you took charge of only on electron. how do you know only 1 electron is involved ?

Hi qea, thank you for the question. Each electron accelerates through the same potential difference. If I understand your thinking, you might be implying that the potential difference is "diluted" by the number of charges, and you're wondering therefore how many charges to use in your calculation? Analogy might be helpful - consider a mass on a cliff that will accelerate through a potential difference after being dropped from the cliff. Each particle of matter accelerates through the same potential difference. You could even imagine that the mass is a bag of marbles just to clarify that the segments of mass are not "pulling each other down".

Since each electron is accelerating through the same potential difference we use only one electron in the calculation. You could use more than one electron if you wish, and you would just have to increase the mass in the denominator appropriately. You would still get the same answer. A single electron achieves the same speed as a collection of electrons in the same way that a single marble dropped from a cliff achieves the same final velocity as the bag of marbles.

Hope this helps,
Shaun

Submitted by qea on Tue, 01/03/2023 - 17:04

link

now i understand. every electrons goes through the same potential difference. thanks!