Question
A battery-operated car utilizes a 12.0 V system. Find the charge the batteries must be able to move in order to accelerate the 750 kg car from rest to 25.0 m/s, make it climb a high hill, and then cause it to travel at a constant 25.0 m/s by exerting a force for an hour.
Final Answer
Solution video
OpenStax College Physics, Chapter 19, Problem 9 (Problems & Exercises)
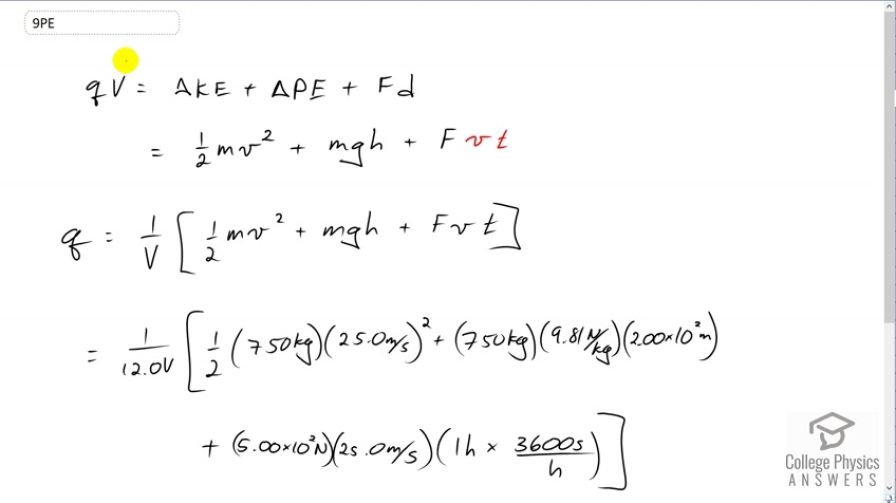
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The charges in this battery have to provide an energy which is going to be equal to the charge multiply by the potential difference of the battery, equal to the change in kinetic energy of the car needed to accelerate it from zero to 25 meters per second and then add to that the change of potential energy as the car is made to climb 200 meters and then the energy needed to make it travel at a constant speed given that there is some drag force against it, and that’s going to be the force multiplied by the distance that it travels. So this is the work done, force times distance, so it’s the energy needed to make it go at a constant altitude at some constant speed. So we can substitute for each of those terms. So the change in kinetic energy is gonna be one half m v final squared, the initial speed being zero, and then add to that, mass times acceleration due to gravity times the change of height for the change in potential energy, and then plus force times the distance but the distance is going to be its speed multiplied by the time that is traveled. And then we’ll divide both sides by potential difference which is 12 Volts because we’re told it’s a 12 Volts battery. So this means the charge is going to be one over the voltage times one half mv squared plus mgh plus vFt. So we have one over 12 Volts times one half times 750 kilograms times the final speed of 25 meters per second squared, plus 750 kilograms times 9.81 newtons per kilogram, gravitational field strength, times two times ten to the two meters, change in height, plus five times ten to the two newtons of force for over this distance, which is a distance of 25 meters per second multiplied by the number of seconds that it’s traveling, which is one hour converted into seconds by multiplying by 3600 seconds per hour. Then we end up with 3.89 times ten to the six Coulombs of charge must travel from the battery to provide the potential energy to do all these things.

