Question
The naturally occurring charge on the ground on a fine
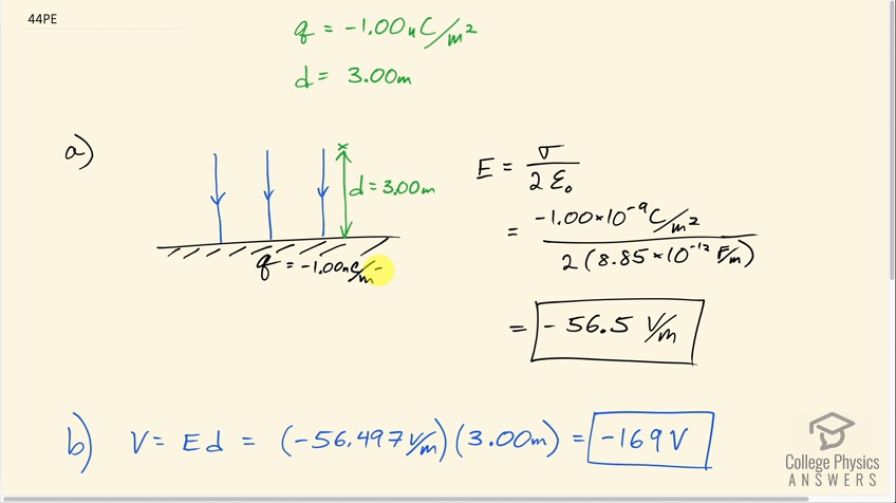
day out in the open country is –1.00 nC/m2 . (a) What is the
electric field relative to ground at a height of 3.00 m? (b) Calculate the electric potential at this height. (c) Sketch electric field and equipotential lines for this scenario.
Final Answer
- It was necessary to consult hyper physics to get the formula for calculating the electric field above a large flat surface with a given charge per surface area.
- The equipotential lines are evenly spaced lines parallel to the ground.
Solution video
OpenStax College Physics, Chapter 19, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
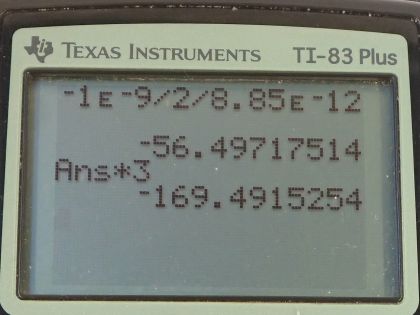
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Imagine that the ground has a charge density of negative 1.00 nanocoulomb per square meter and consider this position here, which is a distance 3.00 meters above the ground, what is the electric field in this area and what is the potential at this position that's the question in part (b), the question in part (a) is what is the electric field strength? So I am not sure how the textbook really is meant to prepare you for this; I had to look up the formula on a website called 'HyperPhysics' and it says that the electric field above a large flat surface is the charge density sigma divided by 2 times the permittivity of free space. So that's negative 1.00 times 10 to the minus 9 coulombs per meter squared divided by 2 times 8.85 times 10 to the minus 12 farads per meter and this gives negative 56.5 volts per meter and the negative sign just indicates that it's downwards since up is positive. Okay! The potential at this position— 3.00 meters above the ground— is going to be the electric field multiplied by the distance because this is a formula you can use when the electric field is uniform, when there is even spacing between the field lines and they are all parallel. And so this is negative 56.497 volts per meter times 3.00 meters which is negative 169 volts. Part (c) asks us to sketch the equipotential lines and they are gonna be lines that are perpendicular to the electric field lines and they will be evenly spaced since the electric field has the same strength in all these positions.