Question
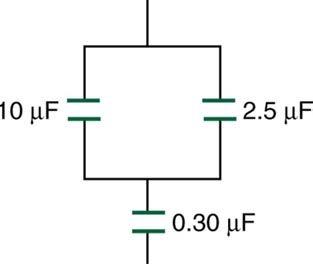
Find the total capacitance of the combination of capacitors in Figure 19.32.
Final Answer
Solution video
OpenStax College Physics, Chapter 19, Problem 57 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
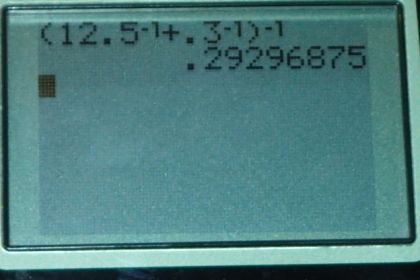
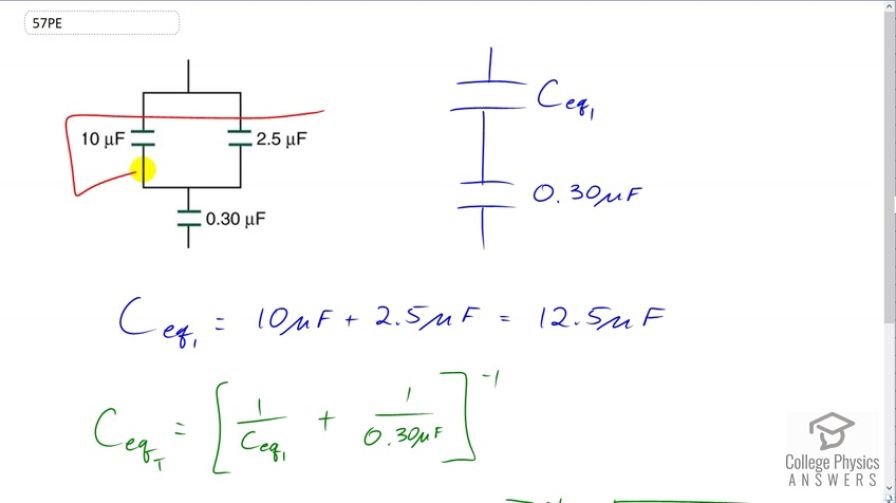
This is College Physics Answers with Shaun Dychko. We're going to find the equivalent capacitance of this circuit, and we'll do it step by step. And, the first step is to combine these two capacitors in parallel and write an equivalent capacitance in this new schematic here. And so, I've copied the 0.03 microfarads unchanged here. And here, I've written capacitance equivalent number one. And, that's going to be the arithmetic sum of these two capacitances because when the capacitors are parallel, as these two are, you add the capacitances directly to get the equivalent capacitance. So, Ceq1 is 12 and a half microfarads. Then, we're going to combine this Ceq1 with the 0.30 microfarads and to do that, we take the reciprocal of each one and add, and then take the reciprocal of that sum. And so, this exponent negative one means take the reciprocal of the result in here. So we have one over 12.5 microfarads plus one over 0.30 microfarads. And then, take the reciprocal of that sum, and we end up with 0.29 microfarads with the equivalent capacitance in total.
Comments
I too got this answer after trying 2.3 micro Farads and the homework said both were wrong. I don't know what's wrong with it it seems right to me.