Question
(a) What is for an electron emerging from the Stanford Linear Accelerator with a total energy of 50.0 GeV? (b) Find its momentum. (c) What is the electron’s wavelength?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 77 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
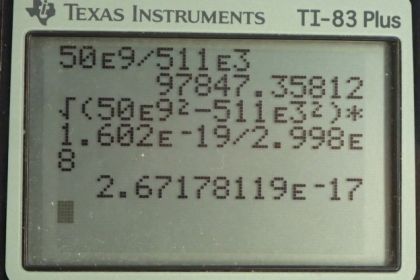
This is College Physics Answers with Shaun Dychko. Electrons are accelerated by the Stanford linear accelerator to an energy of 50 gigaelectron volts and we are asked to figure out, what is the Lorentz factor, gamma, because this is going to be a relativistic speed at that energy and so we need to use our relativistic formula for total energy. This is formula [28.43]. So the total energy is gamma times the rest mass energy and we'll divide both sides by mc squared to get gamma. And so gamma is the total energy divided by the rest mass energy which, we know for an electron, is 511 kiloelectron volts. So we have 50 times 10 to the 9 electron volts energy divided by 511 times 10 to the 3 electron volts—rest mass energy— giving a gamma of 9.78 times 10 to the 4. Part (b) says figure out the momentum. While equation in chapter 28, number 63 says that the total energy squared is the momentum times speed of light squared plus the rest mass energy squared. And so we'll solve this for p. So we'll substract mc squared squared from both sides and then take the square root of both sides and you get pc equals square root of E squared minus mc squared squared and then divide both sides by c. So momentum is the square root of the total energy squared minus the rest mass energy squared all divided by speed of light. Now this, given the units we are using here, we are given units of electron volts, we have to convert that into joules in order to have mks units—meters, kilograms, seconds— in order to match with the units in the denominator for the speed of light, meters per second. So we have the square root of 50 times 10 to the 9 electron volts— total energy squared— minus 511 times 10 to the 3 electron volts squared and square root that and then multiply that by 1.602 times 10 to the minus 19 joules per electron volt so the numerator now has units of joules and we divide that by speed of light, in meters per second, giving us a momentum of 2.67 times 10 to the minus 17 kilogram meters per second. Then part (c) says, find the wavelength. Well, that is Planck's constant divided by momentum. So we are gonna use the answer for part (b) and substitute that here for our momentum using a few extra digits in order to avoid intermediate rounding error and we'll divide Planck's constant by that to get 0.0248 femtometers.