Question
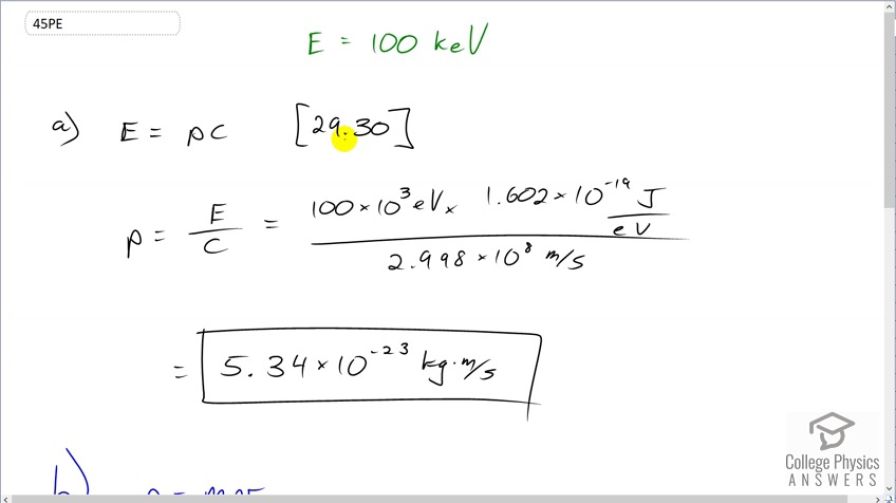
(a) Find the momentum of a 100-keV x-ray photon. (b) Find the equivalent velocity of a neutron with the same momentum. (c) What is the neutron’s kinetic energy in keV?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 45 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
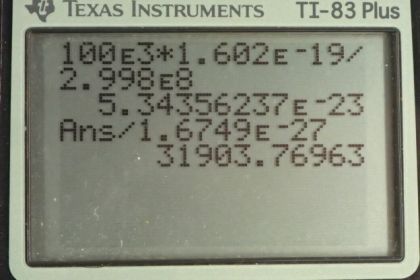
This is College Physics Answers with Shaun Dychko. We are going to find the momentum of a photon that has an energy of 100 kiloelectron volts. So we have this formula [29.30] which says the energy of the photon is its momentum times speed of light and we'll divide both sides by c to get an expression for p. So momentum is energy over speed of light. So that's 100 times 10 to the 3 electron volts multiplied by 1.602 times 10 to the minus 19 joules for every electron volt and we need joules here because joules is an mks unit— meters, kilograms, seconds— which will match with the meters per second that are in the denominator for the speed of light. And so we do that division and we end up with 5.34 times 10 to the minus 23 kilograms meters per second. That's the momentum of the 100 kiloelectron volt photon. Then part (b) says assume a neutron has the same momentum, what would its speed be? So momentum is mass times velocity and we'll assume that the velocity is non-relativistic. So we can divide both sides by m here and the velocity is momentum divided by mass. So that's momentum from part (a) divided by the mass of a neutron— 1.6749 times 10 to the minus 27 kilograms— giving a speed of 31900 meters per second which indeed is non-relativistic. Part (c) says figure out the kinetic energy of this neutron. And so we have one-half mv squared is the kinetic energy so that's one-half mass of the neutron times the speed that we found in part (b) squared. And it says, find the energy in kiloelectron volts. Now these are mks units here and that means when you multiply them, you are going to get joules and so we'll have to convert into electron volts by multiplying by 1 electron volt for every 1.602 times 10 to the minus 19 joules. And then the question says, find it in kiloelectron volts right here. So we have to multiply by 1 kiloelectron volt for every 1000 electron volts. This works out to 5.32 times 10 to the minus 3 kiloelectron volts of kinetic energy.