Question
(a) The lifetime of a highly unstable nucleus is 10−20 s . What is the smallest uncertainty in its decay energy? (b) Compare this with the rest energy of an electron.
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 67 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
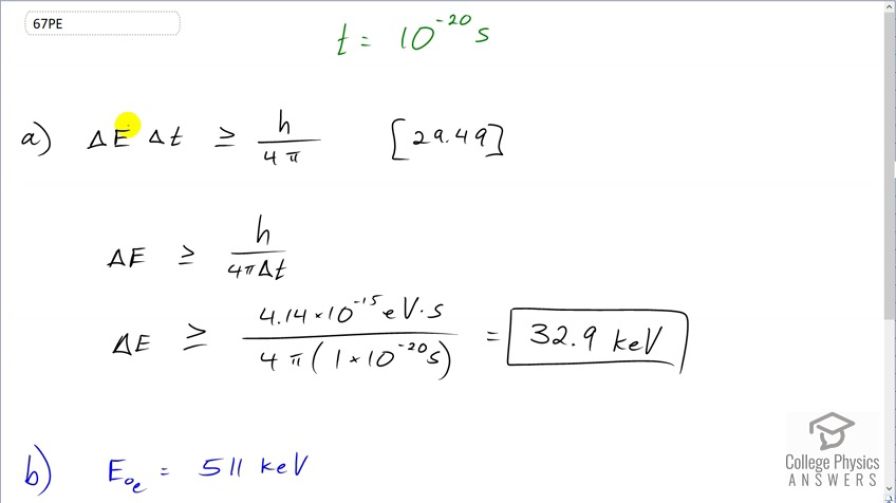
This is College Physics Answers with Shaun Dychko. The lifetime of an unstable nucleus is 10 to the minus 20 seconds and we are asked to figure out, what is the minimum possible uncertainty in its energy? So the Heisenberg uncertainty principle says that the uncertainty in energy times the uncertainty in time has to be more than or equal to Planck's constant over 4π. And so we'll divide both sides by Δt and we get the uncertainty in energy then is at a minimum Planck's constant over 4πΔt. And so to minimize this fraction, we should maximum Δt and take the largest number possible that we can put there which will be the measurement of 10 to the minus 20 seconds. If we knew what the uncertainty in this measurement was or an estimate of the uncertainty, we could plug that in instead. But since we are not given that information, we can just take the entire reading to be the uncertainty such that we can maximize the denominator and therefore minimize this fraction and therefore find the minimum uncertainty in the energy. So we have 4.14 times 10 to the minus 15 electron volt seconds is Planck's constant and we'll divide by 4π times 1 times 10 to the minus 20 seconds giving us 32.9 kiloelectron volts is the minimum uncertainty in the energy. And we are gonna compare that energy to the rest energy of an electron which is 511 kiloelectron volts. So 32.9 over 511 is 6.44 percent.
