Question
(a) Assuming it is nonrelativistic, calculate the velocity of an electron with a 0.100-fm wavelength (small enough to detect details of a nucleus). (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- , which is not possible.
- The assumption that the speed is nonrelativistic is not reasonable.
Solution video
OpenStax College Physics, Chapter 29, Problem 61 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
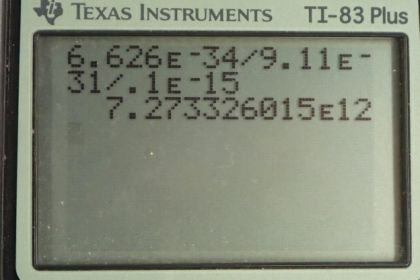
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to assume that an electron with a de Broglie wavelength of 0.0100 femtometers is moving at a non-relativistic speed and let's figure out what that speed is. So the wavelength is Planck's constant divided by momentum and we'll assume momentum is given by the formula—mass times velocity— in the case where the velocity is non-relativistic and replace p with mv here. And now we can solve for v by multiplying both sides by v over λ. And we get that the speed then is Planck's constant divided by mass times wavelength. So that's Planck's constant divided by the mass of an electron times the wavelength of 0.0100 times 10 to the minus 15 meters which gives a speed of 7.27 times 10 to the 12 meters per second. Now that is more than 3 times 10 to the 8 meters per second, which is the speed of light, and so that's not possible—nothing can go faster than the speed of light. And so the assumption that the speed is non-relativistic is not reasonable. We should be using relativistic formula here, in which case, momentum is this Lorentz factor times mass times velocity.