Question
(a) What is the gauge pressure in a car tire containing 3.60 mol of gas in a 30.0 L volume? (b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and ? Assume the temperature returns to and the volume remains constant.
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 37 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
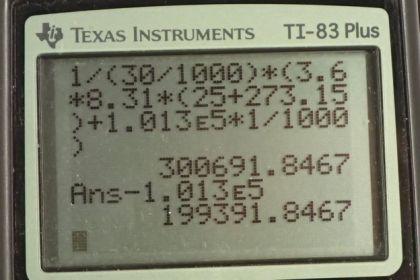
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko Absolute pressure times volume equals the number of moles of gas times the gas constant times the temperature in Kelvin. So we solve for P by dividing both sides by volume and then we'll find the gauge pressure by subtracting atmospheric pressure from the absolute pressure. So we'll substitute n R T over V in place of P. We're given all the information we need to fill in all the variables here. So we're told that there are 3.6 moles of gas times 8.31 joules per mole Kelvin, times the temperature of 25 degrees Celsius converted into Kelvin by adding 273.15. Then divide by 30 liters converted into cubic meters since we need the units to be MKS units here, meters, kilograms, seconds. Then we'll subtract from that 1.013 times ten to the five newtons per square meter and we'll end up with 1.96 times ten to the five newtons per meter squared. That is the gauge pressure. Now in part B, we're told that some gas is added to the tire. So we need to know how many moles have been added. So I have a subscript a here for additional. We're told that this volume of gas that's added when it's at atmospheric pressure outside of the tire, it has a certain volume of one liter and we know the temperature is 25 degrees Celsius and so we'll figure out how many moles are contained in this gas that are added. Then afterwards, we'll say that the pressure inside the tire, its absolute pressure, will be the number of moles of gas initially plus the number of moles that are added times R times temperature divided by the volume. We're told that volume remains constant. So, we'll divide both sides of this by R T to solve for n a. The number of moles added is the atmospheric pressure times the volume of the gas that's added divided by R T and then we substitute that in here in a minute but first, we go absolute pressure is the total number of moles times R T over V and then we'll distribute these factors into the bracket. Then we'll have n I R T over V plus n a R T over V. Here finally, we substitute for the number of moles added. We write P atmosphere times V a over R T times R T over V. The R T's here cancel and then we have a one over V factor that's common between the two and -- what else happened here? I wrote down here what happens after the R T cancels, then I factored out the one over V in this step here. So one over V times initial number of moles times R times temperature, plus atmospheric pressure times the volume added. So we have one over 30 liter volume of the tire converted into cubic meters, times the 3.6 moles of gas initially, times the gas constant, times 25 degrees Celsius converted into Kelvin, plus atmospheric pressure, times the volume added of one liter converted into cubic meters. We end up with this pressure which is absolute pressure and we need to turn it into gauge pressure. So gauge pressure is absolute pressure minus atmospheric pressure. So 3.00692 times ten to the five newtons per square meter minus atmospheric pressure gives us 1.99 times ten to the five newtons per square meter will be the gauge pressure after this gas is added to the tire.