OpenStax College Physics, Chapter 13, Problem 21 (Problems & Exercises)

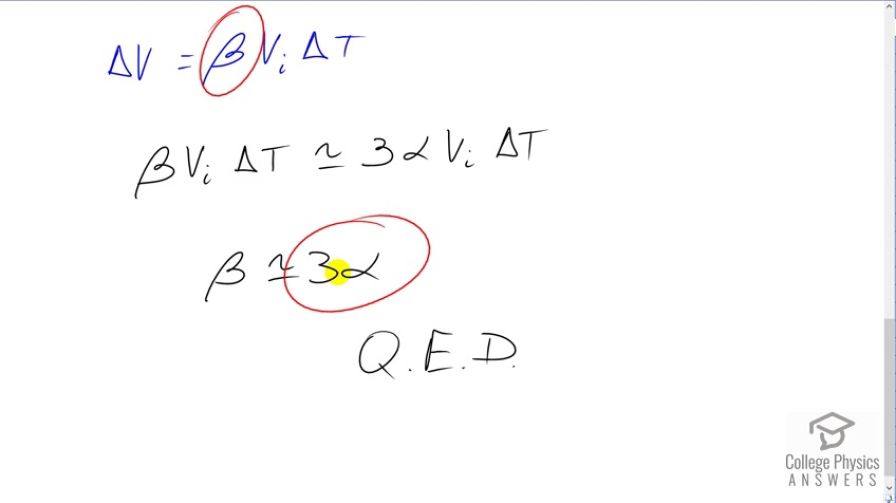
This is College Physics Answers with Shaun Dychko. We're going to show that this volume coefficient of expansion beta is approximately the same as three times the linear coefficient of expansion alpha. But before yet to the conclusion, let's start at the beginning, shall we? We have a change in volume is the final side length of this cube, cubed minus the initial side length cubed. And the final side length will be the initial side length plus the change in length, delta L. And then we're going to cube that sum. So I write that out as three different binomials, and then we'll square the first two which gives us initial link squared plus two times initial length times change in length plus the change in length squared and we will multiply that by this remaining Li plus delta L factor. And multiplying Li by each term in the brackets there gives us Li cubed plus two Li squared delta L plus Li delta L squared plus Li squared delta L. And then plus another term, two Li delta L squared plus delta L cubed. So, basically we're multiplying through by Li and we expect to get this repeated here with an additional Li factor. So we have Li cubed here and then so on and so on. And then we do all that again with delta L. And so we expect another three factors which are here, each containing an additional factor delta L. And then collecting like terms, we have Li cubed minus Li cubed makes zero. And then we have an Li squared delta L term here and another here. And then add in their coefficients two plus one gives us three Li squared delta L. And then likewise we have an Li delta L squared term here and one there giving us three Li delta L squared. And then plus delta L cubed. Now, assuming delta L is small, when we square a small number that makes a really small number, in which case this term becomes negligibly small. And this one is also negligibly small because at delta L cubed. So, all of this approximately equals not with a squiggle here is meant to signify approximately equal to three Li squared delta L. Now, you know delta L is small to the power of one, it's still something that is significant. And so that means delta V which is what all of this is equal to is now three Li squared delta L which is three Li squared and then substituting the equation for change in length in terms of the linear expansion coefficient. So we have alpha initial length times change in temperature. And that makes this three alpha times Li cubed Li squared times Li times delta T. And Li cubed is the initial volume of the cube, so we have three alpha initial volume times change in temperature. Now, the change in volume we're told is also equal to the volume coefficient of expansion times initial volt in delta T. And so that means we can equate these two things. So this is approximately equal to since the change in volume is approximately equal to that. So beta Vi delta T is approximately equal to three alpha Vi delta T. So we can divide both sides by initial volume times change in temperature. And we get beta is approximately equal to three times alpha. So the volume coefficient of expansion is approximately three times the linear coefficient of expansion.