Question
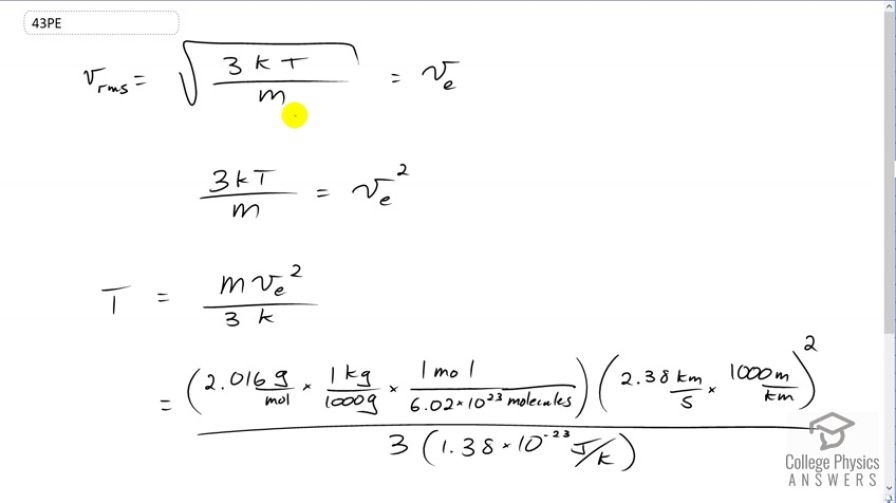
The escape velocity from the Moon is much smaller than from Earth and is only 2.38 km/s. At what temperature would hydrogen molecules (molecular mass is equal to 2.016 g/mol) have an average velocity equal to the Moon’s escape
velocity?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find out at what temperature hydrogen atoms on the moon would have an average velocity equal to the moon's escape velocity. So I have v subscript e for escape here. We'll square both sides and we get three times Boltzmann's constant times absolute temperature divided by mass per hydrogen atom equals the escape velocity squared. Then we'll multiply both sides by m over three k to isolate temperature. So we have temperature is m v e squared over three k. So we substitute in the molar mass of hydrogen molecules here; actually it's not just atoms, these are molecules. This is H two and so the molar mass is 2.016 grams per mole which we have to convert into kilograms per molecule. So multiply this by one kilogram for every 1000 grams and multiply by one mole for every 6.02 times ten to the twenty-three molecules. We end up with some number of kilograms per molecule. We have to do that because our formulas typically expect MKS units, meters, kilograms and seconds. Molecules doesn't really count as a unit. It's just a counting number. So we multiply this by the speed in meters per second. So that's 2.38 kilometers per second we're told is the escape velocity and we multiply that by one thousand meters for every kilometer and we square that and divide by three and then times by Boltzmann's constant in the denominator. We get 458 Kelvin is the temperature at which hydrogen molecules would have the escape velocity of the moon.
