Question
(a) How many moles per cubic meter of an ideal gas are there at a pressure of and at ? (b) What
is unreasonable about this result? (c) Which premise or assumption is responsible?
Final Answer
- This is unreasonably large. Suppose the gas is hydrogen, the density would be . For comparison, the density of uranium, one of the most dense materials found on Earth, is . The hydrogen would be more dense than uranium by a factor of 1000.
- The ideal gas law doesn't apply at such high pressures.
Solution video
OpenStax College Physics, Chapter 13, Problem 69 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
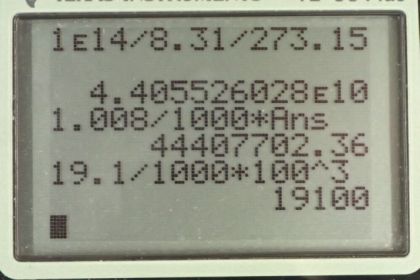
This is College Physics Answers with Shaun Dychko. If we assume the Ideal Gas Law applies here, we can figure out how many moles per cubic meters there are by rearranging PV equals nRT by dividing both sides by VRT. And we get P over RT on one side and over V on the other. And the pressure we're told is one times ten to the 14 pascals divided by 8.31 Joules per Kelvin times zero degrees Celsius written in absolute temperature or Kelvin by adding 273.15 and that gives 4.41 times ten to the ten moles per cubic meter. `This is an unreasonably large number and the reason we know is because let's assume that the gas is Hydrogen, so we can get the lowest possible density calculation. And so, for Hydrogen there's 1.008 grams per mole and then convert that into kilograms by multiplying by one kilogram for every thousand grams. And then multiplied by this moles per cubic meter and we get the density of 4.44 times ten to the seven kilograms per cubic meter. And that's the reason I did that is in order to make comparison to a very very dense solid which is Uranium, I suppose. Uranium is the most dense solids that we have. And if you look up its molar mass in the Appendix a it's 19.1 grams per cubic centimeter, which we'll convert into kilograms per cubic meter and we get 1.91 times ten to the four. And so this Hydrogen is apparently 1000 times more dense than Uranium and that's not realistic. And so, what we're seeing here is that the Ideal Gas Law does not apply at such high pressures because the Ideal Gas Law presumes that there are no interactions between the gas particles. But when they're compressed so much, there ends up being some interactions between them and there might be some repulsion for example. And so it just doesn't apply. The word law is not a very appropriate name actually because it has a lot of exceptions. Normally, laws are things that would be more generalizable.