Question
(a) If the average molecular mass of compounds in food is 50.0 g, how many molecules are there in 1.00 kg of food? (b) How many ion pairs are created in 1.00 kg of food, if it is exposed to 1000 Sv and it takes 32.0 eV to create an ion pair? (c) Find the ratio of ion pairs to molecules. (d) If these ion pairs recombine into a distribution of 2000 new compounds, how many parts per billion is each?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 17 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
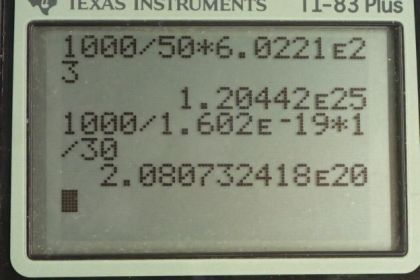
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to estimate the number of molecules there are in a kilogram of food. So the number of molecules will be the mass of food divided by the molar mass that we are given which is 50 grams per mol and then we multiply that by Avogadro's number to get the number of molecules. So the one kilogram has to be converted into grams in order to match with the grams that are in the denominator units. So 1 kilogram times a 1000 grams per kilogram gives a 1000 grams divided by 50 grams per mol and this gives the number of mols and then multiply it by Avogadro's number which has units of molecules per mole. So that's 1.20 times 10 to the 25 molecules in 1 kilogram of food on average. In part (b), we are told that this radiation — and we are not told what type of radiation it is — but we are told that there are 1000 sieverts applied to this kilogram of food and there is one ion pair created for every 30 electron volts of energy absorbed and how many ion pairs are made. So we need to convert the sieverts into units of grays and grays is short for joules per kilogram in order to make this calculation. So in equation [32.6], we are told that the dose equivalent in sieverts equals the absorbed dose in grays times the relative biological effectiveness. Now since we don't know what the type of radiation is, we don't know what the RBE is so let's just assume it's 1 since many types of radiation have relative biological effectiveness of 1. So we divide both sides by this RBE and that's where this number 1 comes from; it's the RBE that we are assuming for this type of radiation and so this works out to 1000 grays. So I have written grays in more base units of joules per kilogram just so you can see how the units cancel. So we multiply the 1000 joules for every kilogram times 1 electron volt for every 1.602 times 10 to the minus 19 joules in order to convert our units into electron volts per kilogram. Then multiply by 1 kilogram and times by 1 ion pair produced for every 30 electron volts giving us 2.08 times 10 to the 20 ion pairs. Part (c) says find the ratio of this to the number of molecules and that works out to 1.7 times 10 to the minus 5 and the reason we are doing this calculations in (c) and (d) is to get a sense of how non-destructive it is to irradiate food as a food safety strategy. And then part (d) says how many parts per billion are there in each of the 2000 compounds that are created when these ion pairs recombine in different ways two thousand different ways. So we have 2.08 times 10 to the 20 ion pairs divided by 2000 compounds times we are multiplying by 1 divided by the number of molecules plus the total number of ion pairs to give us the number of parts because an ion pair is going to combine into a single thing and it's going to combine into a one thing for every this many molecules and pairs and so this is the number of parts per molecule of material that's there and this is true for each of the 2000 compounds. So this part here from here to here is the number of parts per compound per molecule. And we don't want it per molecule because that would be a really small number and so we multiply it by a billion parts in every billion; this is essentially the number 1, it's like saying multiply by a billion divided by a billion but it expresses it in words that are easier to understand and so we end up changing our units to parts per billion by multiplying by this. So we have 8.7 parts per billion per compound. I guess you can say that too. There.