Question
The power output of the Sun is .
(a) If 90% of this is supplied by the proton-proton cycle, how
many protons are consumed per second?
(b) How many neutrinos per second should there be per square meter at the Earth from this process? This huge number is indicative of how rarely a neutrino interacts, since large detectors observe very few per day.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 35 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
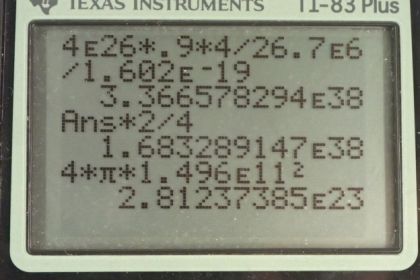
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Sun has a power output of 4 times 10 to the 26 watts and we are told that ninety percent of the fusion reactions that produce this power are the proton-proton cycle. In equation [32.16], tells us the proton cycle produces 26.7 megaelectron volts and it consumes four protons in the process. And part (a) asks us how many protons per second are fusing in this proton-proton cycle to produce this power output? So ninety percent of the power output is attributable to this proton-proton cycle so we multiply the total power output of the Sun by 0.90 and then there are four protons or hydrogen nuclei for every 26.7 times 10 to the 6 electron volts that is writing the prefix mega as times 10 to the 6 here. And then we wanna convert this joules here into electron volts in order to cancel with these electron volts so we have 1 electron volt for every 1.602 times 10 to the minus 19 joules and we end up with number of protons per second and that is 3 times 10 to the 38 protons per second undergo the proton-proton cycle. And the number of neutrino's per second we can calculate by knowing that there are two neutrino's produced for every four protons consumed. And so we can take this number of protons consumed per second that we calculated in part (a) written with a few more decimal place because it is an intermediate calculation and multiplied by two electron neutrino's for every four protons giving us 1.68 times 10 to the 38 neutrino's produced per second. And then we'll divide that by the surface area of a sphere which is at the orbital radius of the Earth and here's the Sun. And then that will give us the number of neutrino's passing through a square meter on Earth every second. So the area of our orbital sphere is 4π times the orbital radius squared. So that's 4π times 1.496 times 10 to the 11 meters squared that gets us area and so we take the total number of neutrino's produced per second in the proton-proton cycle divided by this area and we get 6 times 10 to the 14 neutrino's are passing through every square meter every second on Earth.